Construction of the Incircle of a Triangle

Construction of the Incircle of a Triangle

Incentre

The incentre is (one of the triangle’s points of concurrency formed by) the intersection of the triangle’s three angle bisectors.

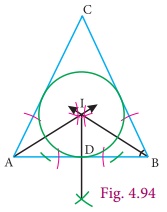
The incentre is the centre of the incircle ; It is usually denoted by I; it is the one point in the triangle whose distances to the sides are equal.

Example 4.15

Construct the incentre of ΔABC with AB = 6 cm, ∠B = 65° and AC = 7 cm Also draw the incircle and measure its radius.

Solution

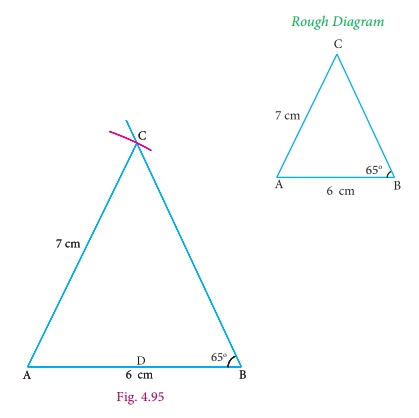
Step 1 : Draw the ΔABC with AB = 6cm, ∠B = 65° and AC = 7cm

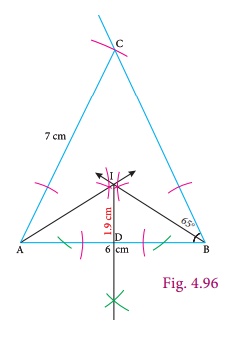
Step 2 : Construct the angle bisectors of any two angles (A and B) and let them meet at I.

Then I  is the incentre of ΔABC. Draw perpendicular from I to any one of the side (AB) to meet AB at D.

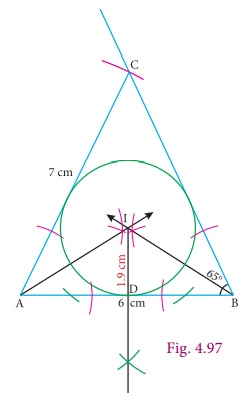
Step 3: With I as centre and ID as radius draw the circle. This circle touches all the sides of the triangle internally.

Step 4: Measure inradius

In radius = 1.9 cm.