Geometry

GEOMETRY

Inspiration is needed in geometry just as much as in poetry.

- Alexander Pushkin

Thales (Pronounced THAYLEES) was born in the Greek city of Miletus. He was known for theoretical and practical understanding of geometry, especially triangles. He used geometry to solve many problems such as calculating the height of pyramids and the distance of ships from the sea shore. He was one of the so-called Seven Sagas or Seven Wise Men of Greece and many regarded him as the first philosopher in the western tradition.

Thales (BC (BCE) 624 – 546)

Learning Outcomes

• To understand theorems on linear pairs and vertically opposite angles.

• To understand the angle sum property of triangle.

• To understand the properties of quadrilaterals and use them in problem solving.

• To understand, interpret and apply theorems on the chords and the angles subtended by arcs of a circle

• To understand, interpret and apply theorems on the cyclic quadrilaterals.

• To construct and locate centroid, orthocentre, circumcentre and incentre of a triangle.

Introduction 

In geometry, we study shapes. But what is there to study in shapes, you may ask. Think first, what are all the things we do with shapes? We draw shapes, we compare shapes, we measure shapes. What do we measure in shapes?

Take some shapes like this:

In both of them, there is a curve forming the shape: one is a closed curve, enclosing a region, and the other is an open curve. We can use a rope (or a thick string) and measure the length of the open curve and the length of the boundary of the region in the case of the closed curve.

Curves are tricky, aren’t they? It is so much easier to measure length of  straight lines using the scale, isn’t it? Consider the two shapes below.

We are going to focus our attention for now only on shapes made using straight lines, and only closed figures. As you will see, there is plenty of interesting things to do already? Fig.4.2 shows an open figure.

We not only want to draw such shapes, we want to compare them, measure them and do much more.  For doing so, we want to describe them. How would you describe these closed shapes? (See Fig 4.3) They are all made of straight lines, all closed.

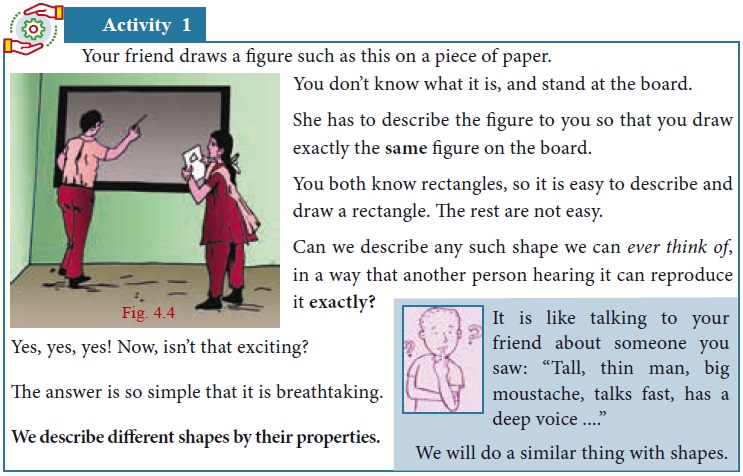
In science we learn that air has certain properties – for instance, it occupies space. Water has the property that it takes the shape of the vessel that contains it, flows from a height to down below. Similarly, triangles, rectangles, circles, and all the shapes we draw, however different they look, have properties that describe them uniquely. By the time you learn Geometry well, you can give shape for everything on earth – indeed (Aadhaar card), not only on earth but anywhere! But for now, have some patience. Just as we started with small numbers and arithmetical operations on them in primary level classes and now you know it is the same for all numbers, similarly we will learn properties of very simple shapes now, and slowly but surely we will learn more and when we are done, you will have techniques to describe any shape in 2 dimensions (like what we draw on paper), or in 3 dimensions (like the solids we use in life), or indeed, in any dimensions.

Why should we bother to learn this? One very practical reason is that all science and engineering demands it. We cannot design buildings, or even tables and chairs, or lay out the circuits inside our mobile phones, without a mathematical understanding of shapes. Another important reason is that geometry gives you a new way of looking at the world, at everything in it. You begin to see that all objects, however complicated they look, are made of very simple shapes. You learn to think not only like a mathematician, but also learn to appreciate symmetry and order, as artists do. Yes, geometry helps you become an artist too.