Statistical Learning Methods

STATISTICAL LEARNING METHODS

Learn probabilistic theories of the world from experience

♦                 We focus on the learning of Bayesian networks

♦                 More specifically, input data (or evidence), learn probabilistic theories of the world (or hypotheses)

View learning as Bayesian updating of a probability distribution over the hypothesis space

H is the hypothesis variable, values h1, h2, . . ., prior P(H) jth observation dj gives the outcome of random variable Dj training data d = d1, . . . , dN

Given the data so far, each hypothesis has a posterior probability:

P(hi|d) = αP(d|hi)P(hi)

where P(d|hi) is called the likelihood

Predictions use a likelihood-weighted average over all hypotheses:

P(X|d) = Σi P(X|d, hi)P(hi|d) = Σi P(X|hi)P(hi|d)

Example

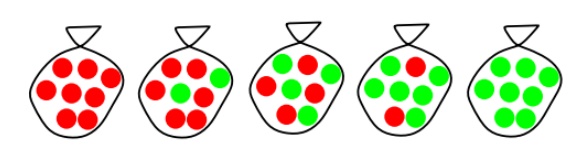
Suppose there are five kinds of bags of candies: 10% are h1: 100% cherry candies

20% are h2: 75% cherry candies + 25% lime candies 40% are h3: 50% cherry candies + 50% lime candies 20% are h4: 25% cherry candies + 75% lime candies 10% are h5: 100% lime candies

Then we observe candies drawn from some bag:

What kind of bag is it? What flavour will the next candy be?

1.The true hypothesis eventually dominates the Bayesian prediction given that the true hypothesis is in the prior

2.The Bayesian prediction is optimal, whether the data set be small or large[?] On the other hand

1.                 The hypothesis space is usually very large or infinite summing over the hypothesis space is often intractable.

2.                 Overfitting when the hypothesis space is too expressive such that some hypotheses fit the date set well.

3.                 Use prior to penalize complexity.