Nature of Physical World and Measurement | Physics - Solved Example Problems | 11th Physics : UNIT 1 : Nature of Physical World and Measurement
Chapter: 11th Physics : UNIT 1 : Nature of Physical World and Measurement
Solved Example Problems
Solved Example Problems for Measurement of length
Example 1.1
From a point on the ground, the top of a tree is seen to have an angle of elevation 60°. The distance between the tree and a point is 50 m. Calculate the height of the tree?
Solution
Angle θ = 60°
The distance between the tree and a point x = 50 m
Height of the tree (h) = ?
For triangulation method tan
h = x tan θ
= 50 × tan 60°
= 50 × 1.732
h = 86.6 m
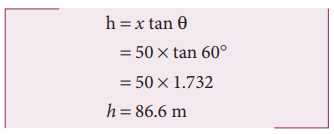
The height of the tree is 86.6 m.
Example 1.2
The Moon subtends an angle of 1° 55’ at the base line equal to the diameter of the Earth. What is the distance of the Moon from the Earth? (Radius of the Earth is 6.4 × 106 m)
Solution
Radius of the Earth = 6.4 × 106 m
From the Figure 1.5 AB is the diameter of the Earth (b)= 2 × 6.4 × 106 m Distance of the Moon from the Earth x = ?
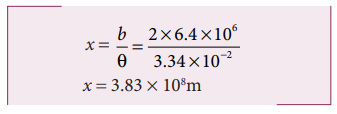
Example 1.3
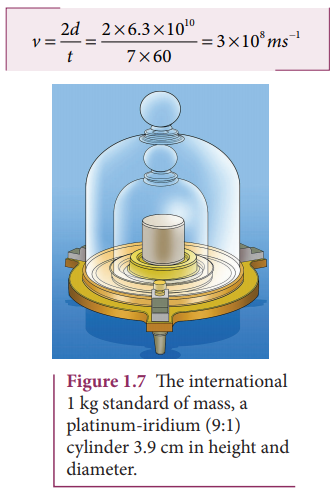
A RADAR signal is beamed towards a planet and its echo is received 7 minutes later. If the distance between the planet and the Earth is 6.3 × 1010 m. Calculate the speed of the signal?
Solution
The distance of the planet from the Earth d = 6.3 × 1010 m
The speed of signal
Solved Example Problems for Error Analysis
Example 1.4
In a series of successive measurements in an experiment, the readings of the period of oscillation of a simple pendulum were found to be 2.63s, 2.56 s, 2.42s, 2.71s and 2.80s. Calculate (i) the mean value of the period of oscillation (ii) the absolute error in each measurement (iii) the mean absolute error (iv) the relative error (v) the percentage error. Express the result in proper form.
Solution
Solved Example Problems for Propagation of errors
(i) Solved Example Problem for Error in the sum of two quantities
Example 1.5
Two resistances R1 = (100 ± 3) Ω, R2 = (150 ± 2) Ω, are connected in series. What is their equivalent resistance?
Solution
Equivalent resistance R = ?
Equivalent resistance R = R1 + R2
(ii) Solved Example Problem for Error in the difference of two quantities
Example 1.6
The temperatures of two bodies measured by a thermometer are t1 = (20 + 0.5)°C, t2 = (50 ± 0.5)°C. Calculate the temperature difference and the error therein.
Solution
(iii) Example Problem for Error in the product of two quantities
Example 1.7
The length and breadth of a rectangle are (5.7 ± 0.1) cm and (3.4 ± 0.2) cm respectively. Calculate the area of the rectangle with error limits.
Solution
(iv) Example Problem for Error in the division or quotient of two quantities
Example 1.8
The voltage across a wire is (100 ± 5)V and the current passing through it is (10±0.2) A. Find the resistance of the wire.
Solution
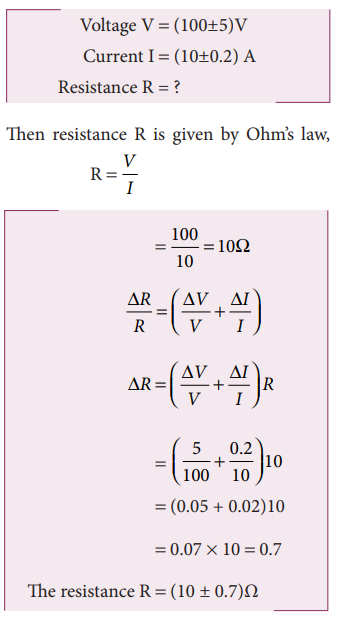
(v) Example Problem for Error in the power of a quantity
Example 1.9
A physical quantity x is given by x
If the percentage errors of measurement in a, b, c and d are 4%, 2%, 3% and 1% respectively then calculate the percentage error in the calculation of x.
Solution
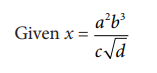
The percentage error in x is given by
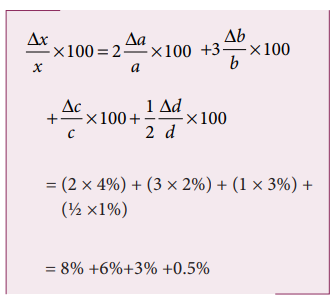
The percentage error is x = 17.5%
Solved Example Problems for Significant Figures
Rules of Significant Figures
Example 1.10
State the number of significant figures in the following
i. 600800
ii. 400
iii. 0.007
iv. 5213.0x
v. 2.65 × 1024 m
vi. 0.0006032
Solution
Solution: i) four ii) one iii) one iv) five v) three vi) four
Rounding Off
Example 1.11
Round off the following numbers as indicated
i) 18.35 up to 3 digits
ii) 19.45 up to 3 digits
iii) 101.55 × 106 up to 4 digits
iv) 248337 up to digits 3 digits
v) 12.653 up to 3 digits.
Solution
i) 18.4 ii) 19.4 iii) 101.6 × 106 iv) 248000 v) 12.7
Addition and subtraction
Example:
1) 3.1 + 1.780 + 2.046 = 6.926
Here the least number of significant digits after the decimal is one. Hence the result will be 6.9.
2) 12.637 - 2.42 = 10.217
Here the least number of significant digits after the decimal is two. Hence the result will be 10.22
Multiplication and Division
Example:
1) 1.21 × 36.72 = 44.4312 = 44.4
Here the least number of significant digits in the measured values is three. Hence the result when rounded off to three significant digits is 44.4
2) 36.72 ÷ 1.2 = 30.6 = 31
Here the least number of significant digits in the measured values is two. Hence the result when rounded off to significant digit becomes 31.
Solved Example Problems for Application of the Method of Dimensional
Analysis
Solved Example Problems
(i) To convert a physical quantity from one system of units to another
Example 1.12
Convert 76 cm of mercury pressure into Nm−2 using the method of dimensions.
Solution
In cgs system 76 cm of mercury pressure = 76 × 13.6 × 980 dyne cm−2
The dimensional formula of pressure P is [ML−1T−2]
Example 1.13
If the value of universal gravitational constant in SI is 6.6x10−11 Nm2 kg−2, then find its value in CGS System?
Solution
Let GSI be the gravitational constant in the SI system and Gcgs in the cgs system. Then
The dimensional formula for G is M−1 L3T −2
(ii) To check the dimensional correctness of a given physical equation
Example 1.14
Check the correctness of the equation
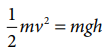
using dimensional analysis method
Solution
Both sides are dimensionally the same, hence the equations
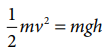
is dimensionally correct.
(iii) To establish the relation among various physical quantities
Example 1.15
Obtain an expression for the time period T of a simple pendulum. The time period T depends on (i) mass ‘m’ of the bob (ii) length ‘l’ of the pendulum and (iii) acceleration due to gravity g at the place where the pendulum is suspended. (Constant k = 2π) i.e
Solution
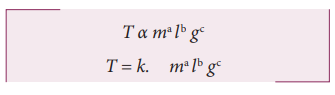
Here k is the dimensionless constant. Rewriting the above equation with dimensions
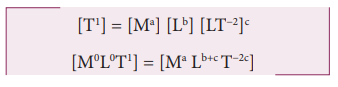
Comparing the powers of M, L and T on both sides, a=0, b+c=0, -2c=1
Solving for a,b and c a = 0, b = 1/2, and c = −1/2
From the above equation T = k. m0 l1/2 g−1/2
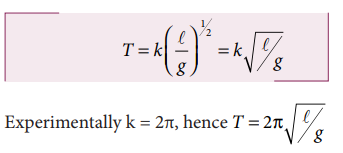
Example 1.16
The force F acting on a body moving in a circular path depends on mass of the body (m), velocity (v) and radius (r) of the circular path. Obtain the expression for the force by dimensional analysis method. (Take the value of k=1)
where k is a dimensionless constant of proportionality. Rewriting above equation in terms of dimensions and taking k = 1, we have
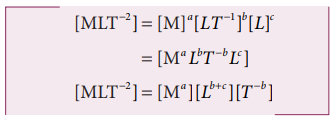
Comparing the powers of M, L and T on both sides
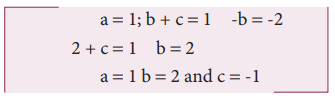
From the above equation we get
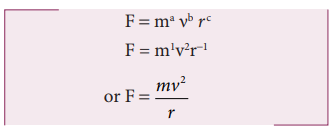
Nature of Physical World and Measurement | Physics
Numerical Problems
1. In a submarine equipped with sonar, the time delay between the generation of a pulse and its echo after reflection from an enemy submarine is observed to be 80 sec. If the speed of sound in water is 1460 ms-1. What is the distance of enemy submarine?
Answers:
The speed of sound in water v = 1460 ms-1
Time taken by the pulse for to and fro :
t = T/2 = 80s/2 = 40s
v = d/t
d = v × T/2 = 1460 × 40
= 58400 m or 58.40 km.
Ans: (58.40 km)
2. The radius of the circle is 3.12 m. Calculate the area of the circle with regard to significant figures.
Answers:
Radius of the circle r = 3.12 m
Area of the circle A = ?
A = πr2 = 3.14 × 3.12 × 3.12 = 30.566016
According to the rule of significant fig,
A = 30.6 m2 [Given data has three sig. fig.]
Ans: (30.6 m 2)
3. Assuming that the frequency γ of a vibrating string may depend upon i) applied force (F) ii) length (l) iii) mass per unit length (m), prove that γa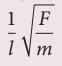 
using dimensional analysis.
Answers:
γ ∝ lm Fb mc
γ = K lm Fb mc
K - dimensionless constant of proportionality
a,b,c - powers of l, F, m
Dimensional Formula of F = [MLT-2]
Dimensional Formula of linear density
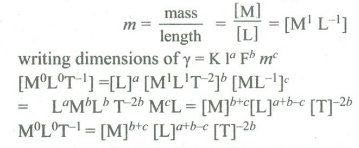
Applying the principle of homogeneity of dimension
b + c = 0 ....(1)
a + b -c = 0 ….. (2)
4. Jupiter is at a distance of 824.7 million km from the Earth. Its angular diameter is measured to be 35.72˝. Calculate the diameter of Jupiter.
Ans: (1.428 × 105 km)
5. The measurement value of length of a simple pendulum is 20 cm known with 2 mm accuracy. The time for 50 oscillations was measured to be 40 s within 1 s resolution. Calculate the percentage accuracy in the determination of acceleration due to gravity ‘g’ from the above measurement.
Answers:
The errors in both Z & T are least count errors.
Ans: (6%)
Related Topics