Chapter: 11th Physics : UNIT 1 : Nature of Physical World and Measurement
Solved Example Problems for Application of the Method of Dimensional Analysis
Solved Example Problems
(i) To convert a physical quantity from one system of units to another
Example 1.12
Convert 76 cm of mercury pressure into Nm−2 using the method of dimensions.
Solution
In cgs system 76 cm of mercury pressure = 76 × 13.6 × 980 dyne cm−2
The dimensional formula of pressure P is [ML−1T−2]

Example 1.13
If the value of universal gravitational constant in SI is 6.6x10−11 Nm2 kg−2, then find its value in CGS System?
Solution
Let GSI be the gravitational constant in the SI system and Gcgs in the cgs system. Then
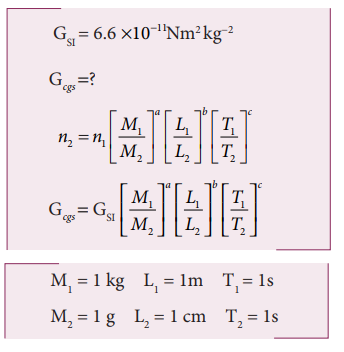
The dimensional formula for G is M−1 L3T −2
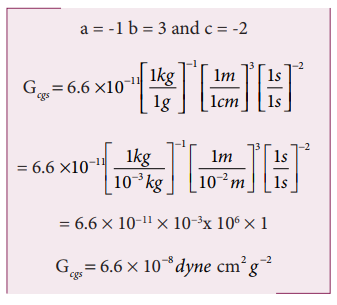
(ii) To check the dimensional correctness of a given physical equation
Example 1.14
Check the correctness of the equation
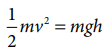
using dimensional analysis method
Solution

Both sides are dimensionally the same, hence the equations
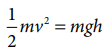
is dimensionally correct.
(iii) To establish the relation among various physical quantities
Example 1.15
Obtain an expression for the time period T of a simple pendulum. The time period T depends on (i) mass ‘m’ of the bob (ii) length ‘l’ of the pendulum and (iii) acceleration due to gravity g at the place where the pendulum is suspended. (Constant k = 2π) i.e
Solution
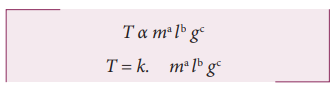
Here k is the dimensionless constant. Rewriting the above equation with dimensions
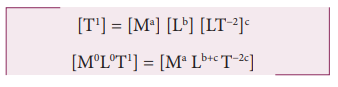
Comparing the powers of M, L and T on both sides, a=0, b+c=0, -2c=1
Solving for a,b and c a = 0, b = 1/2, and c = −1/2
From the above equation T = k. m0 l1/2 g−1/2
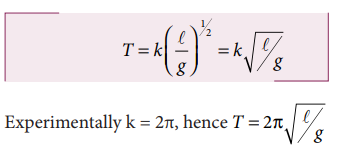
Example 1.16
The force F acting on a body moving in a circular path depends on mass of the body (m), velocity (v) and radius (r) of the circular path. Obtain the expression for the force by dimensional analysis method. (Take the value of k=1)
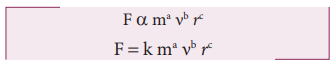
where k is a dimensionless constant of proportionality. Rewriting above equation in terms of dimensions and taking k = 1, we have
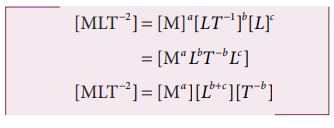
Comparing the powers of M, L and T on both sides
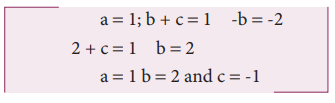
From the above equation we get
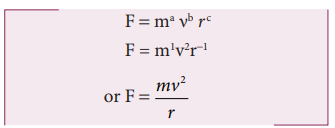
Related Topics