Physics - Application and Limitations of the Method of Dimensional Analysis | 11th Physics : UNIT 1 : Nature of Physical World and Measurement
Chapter: 11th Physics : UNIT 1 : Nature of Physical World and Measurement
Application and Limitations of the Method of Dimensional Analysis
Application
and Limitations of the Method of Dimensional Analysis.
This method is used to
i.
Convert a physical quantity from one system of units to another.
ii.
Check the dimensional correctness of a given physical equation.
iii.
Establish relations among various physical quantities.
i. To convert a physical quantity from one system of units to another
This
is based on the fact that the product of the numerical values (n) and its
corresponding unit (u) is a constant. i.e, n [u] = constant (or) n1[u1]
= n2[u2].
Consider
a physical quantity which has dimension ‘a’
in mass, ‘b’ in length and ‘c’ in time. If the fundamental units in
one system are M1, L1 and T1 and the other
system are M2, L2 and T2 respectively, then we
can write, n1 [M1a L1b T1c]
= n2 [M2a L2b T2c]
We
have thus converted the numerical value of physical quantity from one system of
units into the other system.
(ii) To check the dimensional correctness of a given physical equation
Let
us take the equation of motion
v
= u + at
Apply
dimensional formula on both sides
[LT−1]
= [LT−1] + [LT−2] [T]
[LT−1] = [LT−1] + [LT−1]
(Quantities of same dimension only can be
added)
We
see that the dimensions of both sides are same. Hence the equation is
dimensionally correct.
(iii) To establish the relation among various physical quantities
If
the physical quantity Q depends upon the quantities Q1, Q2
and Q3 ie. Q is proportional to Q1, Q2 and Q3.
Then,
Q α Q1a Q2b
Q3c
Q
= k Q1a Q2b Q3c
where
k is a dimensionless constant. When the dimensional formula of Q, Q1,
Q2 and Q3 are substituted, then according to the
principle of homogeneity, the powers of M, L, T are made equal on both sides of
the equation. From this, we get the values of a, b, c
Limitations of Dimensional analysis
This
method gives no information about the dimensionless constants in the formula
like 1, 2, ……..π,e, etc.
This
method cannot decide whether the given quantity is a vector or a scalar.
This
method is not suitable to derive relations involving trigonometric, exponential
and logarithmic functions.
It
cannot be applied to an equation involving more than three physical quantities.
It
can only check on whether a physical relation is dimensionally correct but not
the correctness of the relation. For
example using dimensional
analysis, s = ut + 1/3 at2 is
dimensionally correct whereas the correct relation is s = ut + 1/2 at2.
Solved Example Problems
(i) To convert a physical quantity from one system of units to another
Example 1.12
Convert 76 cm of mercury pressure into Nm−2 using the method of dimensions.
Solution
In cgs system 76 cm of mercury pressure = 76 × 13.6 × 980 dyne cm−2
The dimensional formula of pressure P is [ML−1T−2]

Example 1.13
If the value of universal gravitational constant in SI is 6.6x10−11 Nm2 kg−2, then find its value in CGS System?
Solution
Let GSI be the gravitational constant in the SI system and Gcgs in the cgs system. Then
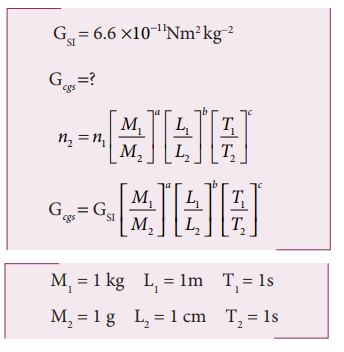
The dimensional formula for G is M−1 L3T −2
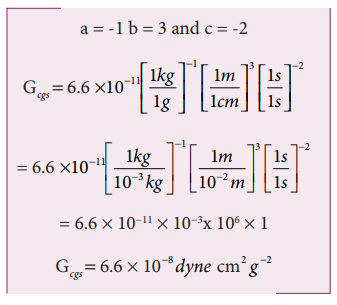
(ii) To check the dimensional correctness of a given physical equation
Example 1.14
Check the correctness of the equation
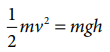
using dimensional analysis method
Solution

Both sides are dimensionally the same, hence the equations
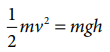
is dimensionally correct.
(iii) To establish the relation among various physical quantities
Example 1.15
Obtain an expression for the time period T of a simple pendulum. The time period T depends on (i) mass ‘m’ of the bob (ii) length ‘l’ of the pendulum and (iii) acceleration due to gravity g at the place where the pendulum is suspended. (Constant k = 2π) i.e
Solution
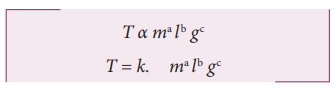
Here k is the dimensionless constant. Rewriting the above equation with dimensions
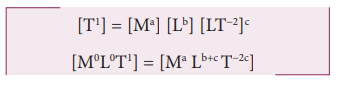
Comparing the powers of M, L and T on both sides, a=0, b+c=0, -2c=1
Solving for a,b and c a = 0, b = 1/2, and c = −1/2
From the above equation T = k. m0 l1/2 g−1/2
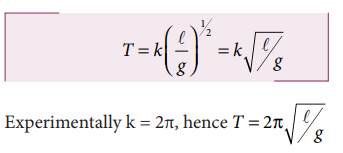
Example 1.16
The force F acting on a body moving in a circular path depends on mass of the body (m), velocity (v) and radius (r) of the circular path. Obtain the expression for the force by dimensional analysis method. (Take the value of k=1)
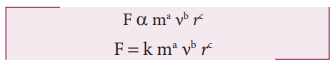
where k is a dimensionless constant of proportionality. Rewriting above equation in terms of dimensions and taking k = 1, we have
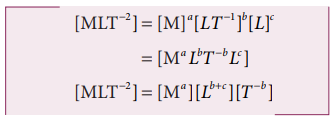
Comparing the powers of M, L and T on both sides
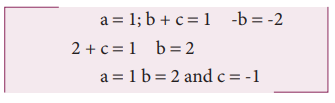
From the above equation we get

Related Topics