Theory of Errors | Physics - Propagation of errors | 11th Physics : UNIT 1 : Nature of Physical World and Measurement
Chapter: 11th Physics : UNIT 1 : Nature of Physical World and Measurement
Propagation of errors
Propagation
of errors
A
number of measured quantities may be involved in the final calculation of an
experiment. Different types of instruments might have been used for taking
readings. Then we may have to look at the errors in measuring various quantities,
collectively.
The
error in the final result depends on
i.
The errors in the individual measurements
ii.
On the nature of mathematical operations performed to get the final result. So
we should know the rules to combine the errors.
The
various possibilities of the propagation or combination of errors in different
mathematical operations are discussed below:
i. Error in the sum of two quantities
Let
∆A and ∆B be the absolute errors in the two quantities A and B respectively.
Then,
Measured
value of A = A ± ∆A
Measured
value of B = B ± ∆B
Consider
the sum, Z = A + B
The
error ∆Z in Z is then given by
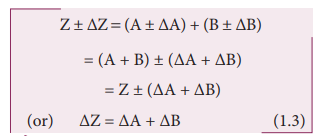
ii. Error in the difference of two quantities
Let ΔA and ΔB be the absolute
errors in the two quantities, A and B, respectively. Then,
Measured value of A = A ± ΔA
Measured value of B = B ± ΔB
Consider the difference, Z = A – B
The error ΔZ in Z is then given by
Z ± ΔZ = (A ± ΔA) – (B ± ΔB)
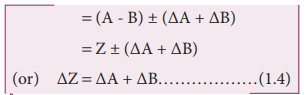
(iii) Error in the product of two quantities
Let ΔA and ΔB be the absolute
errors in the two quantities A, and B, respectively. Consider the product Z =
AB
The error ΔZ in Z is given by Z ±
ΔZ = (A ± ΔA) (B ± ΔB)
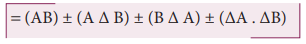
Dividing L.H.S by Z and R.H.S by
AB, we get,
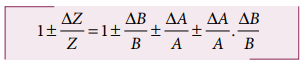
As ΔA /A, ΔB / B are
both small quantities, their product term
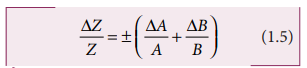
(iv) Error in the division or quotient of two quantities
Let ΔA and ΔB be the
absolute errors in the two quantities A and B respectively.
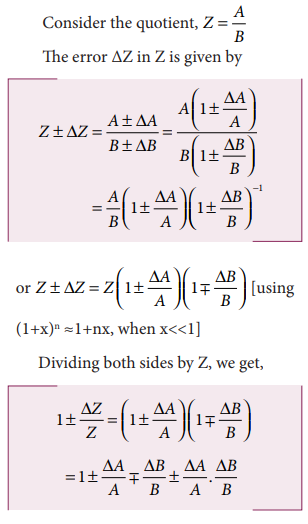
As the terms ΔA/A and
ΔB/B are small, their product term can be neglected.
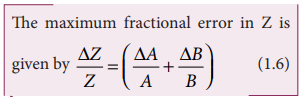
(v) Error in the power of a quantity
Consider the nth
power of A, Z = An The
error ΔZ in Z is given by

We get [(1+x)n
≈1+nx, when x<<1] neglecting remaining terms, Dividing both sides by Z
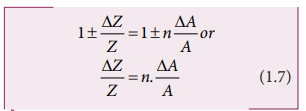

(i) Example Problem for Error in the sum of two quantities
Example 1.5
Two resistances R1 = (100 ± 3) Ω, R2 = (150 ± 2) Ω, are connected in series. What is their equivalent resistance?
Solution
Equivalent resistance R = ?
Equivalent resistance R = R1 + R2

Example 1.5
Two resistances R1 = (100 ± 3) Ω, R2 = (150 ± 2) Ω, are connected in series. What is their equivalent resistance?
Solution
Equivalent resistance R = ?
Equivalent resistance R = R1 + R2

(ii) Example Problem for Error in the difference of two quantities
Example 1.6
The temperatures of two bodies measured by a thermometer are t1 = (20 + 0.5)°C, t2 = (50 ± 0.5)°C. Calculate the temperature difference and the error therein.
Solution

Example 1.6
The temperatures of two bodies measured by a thermometer are t1 = (20 + 0.5)°C, t2 = (50 ± 0.5)°C. Calculate the temperature difference and the error therein.
Solution

(iii) Example Problem for Error in the product of two quantities
Example 1.7
The length and breadth of a rectangle are (5.7 ± 0.1) cm and (3.4 ± 0.2) cm respectively. Calculate the area of the rectangle with error limits.
Solution

Example 1.7
The length and breadth of a rectangle are (5.7 ± 0.1) cm and (3.4 ± 0.2) cm respectively. Calculate the area of the rectangle with error limits.
Solution

(iv) Example Problem for Error in the division or quotient of two quantities
Example 1.8
The voltage across a wire is (100 ± 5)V and the current passing through it is (10±0.2) A. Find the resistance of the wire.
Solution
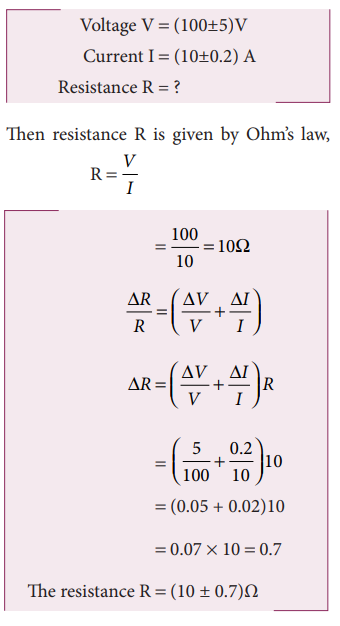
Example 1.8
The voltage across a wire is (100 ± 5)V and the current passing through it is (10±0.2) A. Find the resistance of the wire.
Solution
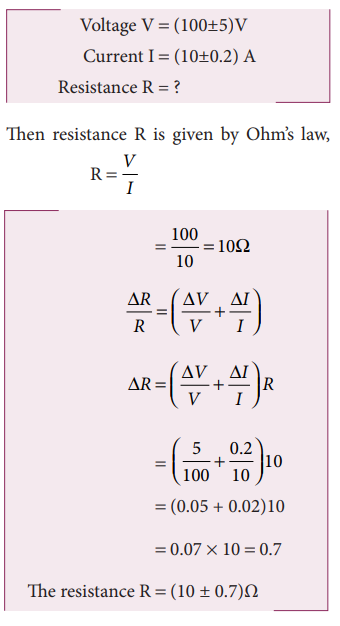
(v) Example Problem for Error in the power of a quantity
Example 1.9
A physical quantity x is given by x
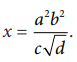
If the percentage errors of measurement in a, b, c and d are 4%, 2%, 3% and 1% respectively then calculate the percentage error in the calculation of x.
Solution

The percentage error in x is given by

The percentage error is x = 17.5%
Example 1.9
A physical quantity x is given by x
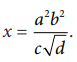
If the percentage errors of measurement in a, b, c and d are 4%, 2%, 3% and 1% respectively then calculate the percentage error in the calculation of x.
Solution

The percentage error in x is given by

The percentage error is x = 17.5%
Related Topics