Significant Figures

SIGNIFICANT FIGURES

Definition and Rules of Significant Figures

The digits which tell us the number of units we are reasonably sure of having counted in making a measurement are called significant figures.

The digits that are known reliably plus the first uncertain digit are known as significant figures or significant digits.

For example, the value of gravitational constant is 6.67 × 10⁻¹¹ N m² kg⁻². Here the digits 6 and 6 are reliable and certain, while the digit 7 is uncertain. Thus the measured value has three significant figures.

The rules for counting significant figures are given in Table 1.9.

Example 1.10

State the number of significant figures in the following

i.        600800

ii.       400

iii.      0.007

iv.      5213.0x

v.       2.65 × 1024 m

vi.      0.0006032

Solution

Solution: i) four ii) one iii) one iv) five v) three vi) four

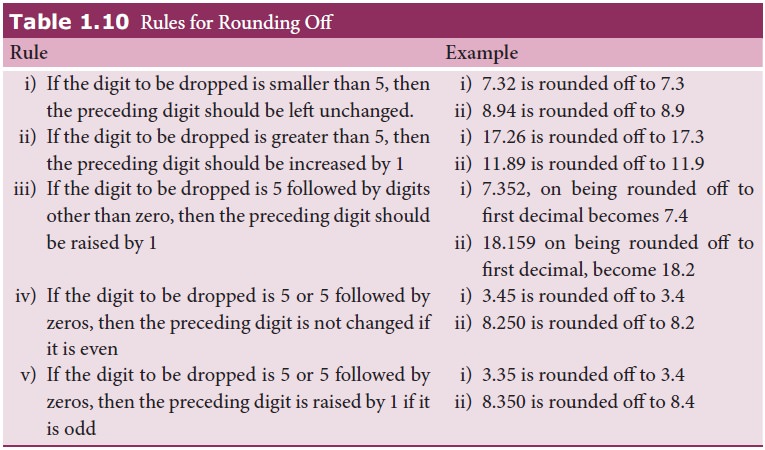
Rounding Off

Calculators are widely used now-a-days to do calculations. The result given by a calculator has too many figures. In no case should the result have more significant figures than the figures involved in the data used for calculation. The result of calculation with numbers containing more than one uncertain digit should be rounded off. The rules for rounding off are shown in Table 1.10.

Example 1.11

Round off the following numbers as indicated

i) 18.35 up to 3 digits

ii) 19.45 up to 3 digits

iii) 101.55 × 106 up to 4 digits

iv) 248337 up to digits 3 digits

v) 12.653 up to 3 digits.

Solution

i) 18.4 ii) 19.4 iii) 101.6 × 106 iv) 248000 v) 12.7

Arithmetical Operations with Significant Figures

i. Addition and subtraction

In addition and subtraction, the final result should retain as many decimal places as there are in the number with the smallest number of decimal places.

Example:

1) 3.1 + 1.780 + 2.046 = 6.926

Here the least number of significant digits after the decimal is one. Hence the result will be 6.9.

2) 12.637 - 2.42 = 10.217

Here the least number of significant digits after the decimal is two. Hence the result will be 10.22

ii. Multiplication and Division

In multiplication or division, the final result should retain as many significant figures as there are in the original number with smallest number of significant figures.

Example:

1) 1.21 × 36.72 = 44.4312 = 44.4

Here the least number of significant digits in the measured values is three. Hence the result when rounded off to three significant digits is 44.4

2) 36.72 ÷ 1.2 = 30.6 = 31

Here the least number of significant digits in the measured values is two. Hence the result when rounded off to significant digit becomes 31.