Long Answer Questions

Nature of Physical World and Measurement | Physics

Long Answer Questions

1. i) Explain the use of screw gauge and vernier caliper in measuring smaller distances.

ii) Write a note on triangulation method and radar method to measure larger distances.

i) Measurement of small distances :

Screw gauge and Vernier caliper:

Screw gauge:

● The screw gauge is an instrument used for measuring accurately the dimensions of objects up to a maximum of about 50 mm.

● The principle of the instrument is the magnification of linear motion using the circular motion of a screw.

● The least count of the screw gauge is 0.01 mm.

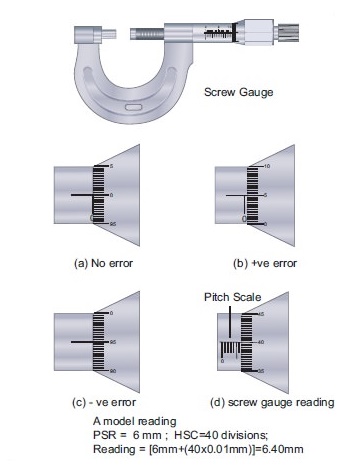
Vernier caliper:

● A vernier caliper is a versatile instrument for measuring the dimensions of an object namely diameter of a hole, or a depth of a hole.

● The least count of the vernier caliper is 0.1 mm.

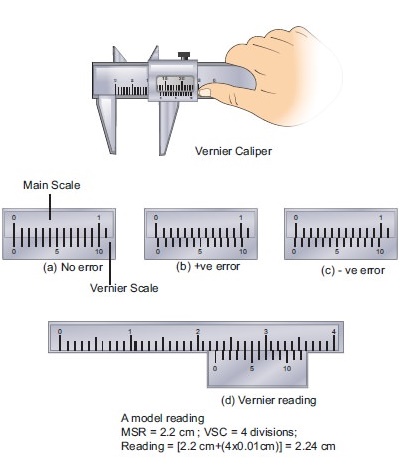
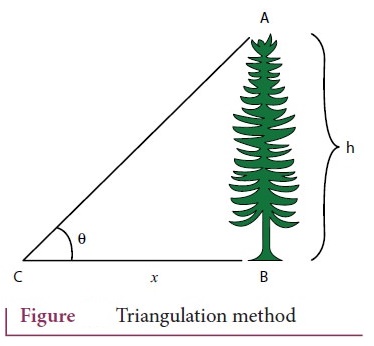
ii) Triangulation method for the height of an accessible object

● Let AB=h be the height of the tree or tower to be measured. Let C be the point of observation at distance x from place a range finder at C and measure the angle of elevation. <ABC = θ as shown in Figure.

● From right angled triangle ABC.

tan θ = AB / ВС = h / x .

 (or)

height h = x tan

Knowing its distance x, the height h can be determined.

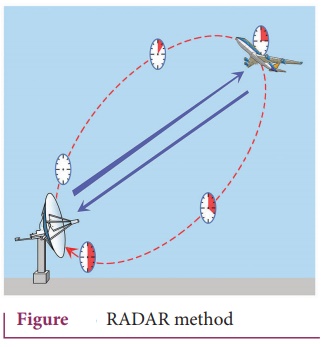
Radar method

● The word RADAR stands for Radio Detection and Ranging. A radar can be used to measure accurately the distance of a nearby planet such as Mars.

● In this method, radio waves are sent from transmitters, after reflection from the planet, they are detected by the receiver.

● By measuring, the time interval (t) between the instants the radio waves are sent and received, the distance of the planet can be determined as

Speed = distance travelled / time taken

Distance(d) = Speed of radio waves × time taken

d = [v × t] / 2

This method can also be used to determine the height, at which an aeroplane flies from the ground.

2. Explain in detail the various types of errors.

The uncertainty in a measurement is called an error. Random error, systematic error and gross error are the three possible errors.

i) Systematic errors

● Systematic errors are reproducible inaccuracies that are consistently in the same direction.

These occur often due to a problem that persists throughout the experiment. Systematic errors can be classified as follows.

1) Instrumental errors

● When an instrument is not calibrated properly at the time of manufacture, instrumental errors may arise.

● If a measurement is made with a meter scale whose end is worn out, the result obtained will have errors.

● These errors can be corrected by choosing the instrument carefully.

2) Imperfections in experimental technique or procedure

● These errors arise due to the limitation in the experimental arrangement.

● As an example while performing experiments with a calorimeter, if there is no proper insulation, there will be radiation losses. 

● This results in errors and to overcome these, necessary correction has to be applied.

3) Personal errors

These errors are due to individuals performing the experiment, may be due to incorrect initial setting up of the experiment or carelessness of the individual making the observation due to improper precautions.

4) Errors due to external causes

The change in the external conditions during an experiment can cause error in measurement. For example, change in temperature, humidity, or pressure during measurements may affect the result of the measurement.

5) Least count error

Least count is the smallest value that can be measured by the measuring instrument, and the error due to this measurement is least count error. Least count error can be reduced by using a high precision instrument for the measurement.

ii) Random errors:

● Random error may arise due to random and unpredictable variations in experimental conditions like pressure, temperature, voltage supply etc.

● Errors may also be due to personal errors by the observer who performs the experiment. Random errors are sometimes called "chance error".

● When different readings are obtained by a person every time he repeats the experiment, personal error occurs.

● If number of trial readings are taken in an experiment.

● The readings are a1, a2, a2, ….. an.

The arithmetic mean is

 = [ a1 + a2 + a3 + …….. an ] / n

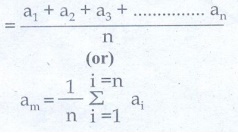
iii) Gross errors:

● The error caused due to shear carelessness of an observer is called gross error.

Ex:

● Taking reading without setting instrument properly.

● Taking observation in wrong manner

● Recording wrong observation.

● Using wrong values in calculation

These errors can be minimized only when an observer is careful and mentally alert.

3. What do you mean by propagation of errors? Explain the propagation of errors in addition and multiplication.

Propagation of errors

A number of measured quantities may be involved in the final calculation of an experiment. Different type of instruments might have been used for taking readings. Then we may have to look at the errors in measuring various quantities, collectively.

The error in the final result depends on

i) The errors in the individual measurements

ii) On the nature of mathematical operations performed to get the final result. So we should know the rules to combine the errors. .

The various possibilities of the propagation of combination of errors in different mathematical operations are discussed below: 

(i) Error in the sum of two quantities

Let ΔA and ΔB be the absolute errors in the two quantities A and B respectively. Then,

Measured value of A = A ± ΔA

Measured value of B = B ± ΔB

Consider the sum, Z= A ± B

The error ΔZ in Z is then given by

Z ± ΔZ = (A+A) + (B ± ΔB)

 = (A+B) ± (ΔA + ΔB)

 = Z ± (ΔA + ΔB)

(or) ΔZ = ΔA + ΔB

The maximum possible error in the sum of two quantities is equal to the sum of the absolute errors in the individual quantities.

ii) Error in the product of two quantities.

Let ∆A and ∆B be the absolute errors in the two quantities A, and B, respectively. Consider the product Z=AB

The error ∆Z in Z is given by Z ± ∆Z = (A ± ∆A) (B ± ∆B)

= (AB) ± (A∆B) ± (B∆A) ± (∆A. ∆B)

Dividing L.H.S by Z and R.H.S by AB, we get,

1 ± ∆Z/Z = ± ∆B/B ± ∆A/A ± ∆A/A ∆B/B

As ∆A / A, ∆B / B are both small quantities, their product term ∆A/A ∆B/B can be neglected. The maximum fractional error in Z is ∆Z / Z = ± (∆A/A + ∆B/B)

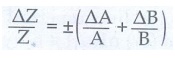
The maximum fractional error in the product of two quantities is equal to the sum of the fractional errors in the individual quantities.

4. Write short notes on the following.

a) Unit

b) Rounding - off

c) Dimensionless quantities

a) Unit: An arbitrarily chosen standard of measurement of a quantity, which is accepted internationally is called unit of the quantity.

b) Rounding off: Calculators are widely used now-a-days to do calculations. The result given by a calculator has too many figures. In no case should the result have more significant figures than the figures involved in the data used for calculation. The result of calculation with numbers containing more than one uncertain digit should be rounded off.

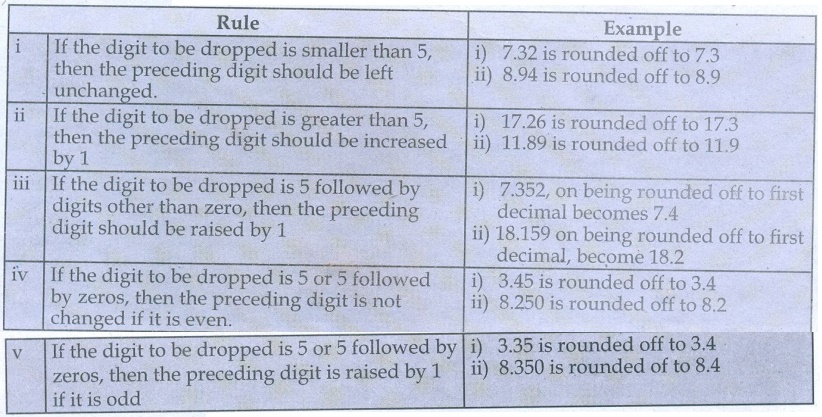
Rules for Rounding off :

Rule

i If the digit to be dropped is smaller than 5, then the preceding digit should be left unchanged. Example: i) 7.32 is rounded off to 7.3 ii) 8.94 is rounded off to 8.9

ii If the digit to be dropped is greater than 5, then the preceding digit should be increased by 1. Example: i) 17.26 is rounded off to 17.3 ii) 11.89 is rounded off to 11.9

iii If the digit to be dropped is 5 followed by digits other than zero, then the preceding digit should be raised by 1. Example: i) 7.352, on being rounded off to first decimal becomes 7.4 ii) 18.159 on being rounded off to first decimal, become 18.2

iv. If the digit to be dropped is 5 or 5 followed by zeros, then the preceding digit is not changed if it is even. Example: i) 3.45 is rounded off to 3.4 ii) 8.250 is rounded off to 8.2

v. If the digit to be dropped is 5 or 5 followed by zeros, then the preceding digit is raised by 1 if it is odd. Example: i) 3.35 is rounded off to 3.4 ii) 8.350 is rounded of to 8.4

c) Dimension Quantities, Dimensionless Quantities.

i) Dimensionless Variables : Physical quantities which have no dimensions, but have variable values are called dimensionless variables. Examples are specific gravity, Strain, refractive index etc.

ii) Dimensionless constant: Quantities which have constant values and also have no dimensions are called dimensionless constants. Examples are π, e, numbers etc.

5. Explain the principle of homogeniety of dimensions. What are its uses? Give example.

Principle of homogeneity of dimensions:

The principle of homogeneity of dimensions states that the dimensions of all the terms in a physical expression should be the same.

For example, in the physical expression v2 = u2+2as the dimensions of v2, u2 and 2as are the same and equal to [L2T-2]

Uses : This method is used to

(i) Convert a physical quantity from one system of units to another.

(ii) Check the dimensional correctness of a given physical equation.

(iii) Establish relations among various physical quantities.

(i) To Convert a physical quantity from one system of units to another.

This is based on the fact that the product of the numerical values (n) and its corresponding uint (u) is a constant. i.e. n (u) = constant (or) n1(u1) = n2 (y2)

Consider a physical quantity which has dimension 'a' in mass, 'b' in length an 'c' in time. If the fundamental units in one system are M1, L1, and T1 and the other system are M2, L2 and T2 respectively, then we can write, n1(M1aL 1bT1c) = n2 (M1aL 1bT1c)

Example : Convert 76cm of mercury pressure into Nm-2 using the method of dimensions.

Solution: In cgs system 76cm of mercury pressure = 76 × 13.6 × 980 dyne cm−2

The dimensional formula of pressure P is (ML−1T−2)

P1 [M1aL 1bT1c] = P2 [M2aL2bT2c ]

We hawe P2 = P1 [M1/M2]a [L1/L2]b [T1/T2]c

M1 = 1g, M2 = 1kg

L1 = 1cm, L2 = 1m

T1 = 1s, T2 = 1s

So a = 1, b = −1, and c = −2

Then

P2 = 76 × 13.6 × 980 [ 1g / 1kg ]1[ 1cm / 1m ]-1[ 1s/1s]-2

= 76 × 13.6 × 980 × [10-3 kg / 1kg][10-2m / 1m ][1s /1s] -2

= 76 × 13.6 × 980 × [10-3] × 102

P2 = 1.01 × 105 Nm-2

ii) To check the dimensional correctness of a given physical equation

Let us take the equation of motion, v = u + at

Apply dimensional formula on both sides

[LT−1] = LT−1] + [LT−2] [T]

[LT−1] = [LT−1] + [LT−1]

(Quantities of same dimension only can be added)

The dimensions of both sides are same. Hence the equation is dimensionally correct.

Example: Obtain an expression for the time period T of a simple pendulum. The time period T depend upon (i) mass 'm' of the bob (ii) length ‘l’ of the pendulum and (iii) acceleration due to gravity 'g’ at the place where the pendulum is suspended. (Constant k = 2 π) i.e.

Solution: T ∝ ma lb gc

T = k. ma lb gc

Here k is the dimensionless constant. Rewriting the above equation with dimensions.

[T1] = [Ma] [Lb] [Tc]

[M°L°T1] = [MaLb+cT−2c]

Comparing the powers of M, L and T on both sides, a=0, b+c = 0, −2c = l

Solving for a, b and c, a = 0, b = 1/2, and c = −1/2

From the above equation T = k. m° l1/2 g-1/2

T = k(l/g)1/2 = k √(l/g)

Experimentally k = 2 π , hence T = 2π √ (l/g)