Chapter: 11th Physics : UNIT 1 : Nature of Physical World and Measurement
Solved Example Problems for Physics: Nature of Physical World and Measurement
Numerical Problems
1. In a submarine equipped with sonar, the time delay between the generation of a pulse and its echo after reflection from an enemy submarine is observed to be 80 sec. If the speed of sound in water is 1460 ms-1. What is the distance of enemy submarine?
Answers:
The speed of sound in water v = 1460 ms-1
Time taken by the pulse for to and fro :
t = T/2 = 80s/2 = 40s
v = d/t
d = v × T/2 = 1460 × 40
= 58400 m or 58.40 km.
Ans: (58.40 km)
2. The radius of the circle is 3.12 m. Calculate the area of the circle with regard to significant figures.
Answers:
Radius of the circle r = 3.12 m
Area of the circle A = ?
A = πr2 = 3.14 × 3.12 × 3.12 = 30.566016
According to the rule of significant fig,
A = 30.6 m2 [Given data has three sig. fig.]
Ans: (30.6 m 2)
3. Assuming that the frequency γ of a vibrating string may depend upon i) applied force (F) ii) length (l) iii) mass per unit length (m), prove that γa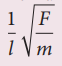 
using dimensional analysis.
Answers:
γ ∝ lm Fb mc
γ = K lm Fb mc
K - dimensionless constant of proportionality
a,b,c - powers of l, F, m
Dimensional Formula of F = [MLT-2]
Dimensional Formula of linear density
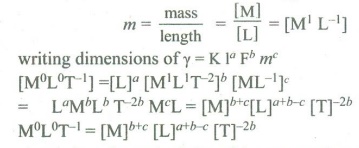
Applying the principle of homogeneity of dimension
b + c = 0 ....(1)
a + b -c = 0 ….. (2)
4. Jupiter is at a distance of 824.7 million km from the Earth. Its angular diameter is measured to be 35.72˝. Calculate the diameter of Jupiter.
Ans: (1.428 × 105 km)
5. The measurement value of length of a simple pendulum is 20 cm known with 2 mm accuracy. The time for 50 oscillations was measured to be 40 s within 1 s resolution. Calculate the percentage accuracy in the determination of acceleration due to gravity ‘g’ from the above measurement.
Answers:
The errors in both Z & T are least count errors.
Ans: (6%)
Conceptual Questions
1. Why is it convenient to express the distance of stars in terms of light year (or) parsec rather than in km?
Answer:
The distances of astronomical objects like stars, planets etc from the earth are huge. The distance on the earth are relatively small so it can be measured in km.
For Example :
The distance to be next nearest big galaxy Andromeda is 21,000,000,000,000,000,000 km. i.e. 21 × 1018 km.
This number is so large that it becomes hard to write and to interpret.
So astronomical units like light year, parsec A.U are used for large distances.
2. Show that a screw gauge of pitch 1 mm and 100 divisions is more precise than a vernier caliper with 20 divisions on the sliding scale.
Answers
Least count of screw gauge
So screw gauge is more precise than vernier.
3. If humans were to settle on other planets which of the fundamental quantities will be in trouble? Why?
Answers:
Time will be in trouble. Time becomes irrelevant. Because day and year based on spinning and revolution of the planet. So each planet has its own year length.
Eg. : Uranus and Neptune move too slow.
4. Having all units in atomic standards is more useful. Explain.
Answers:
All units in atomic standards are more useful because they never change with time.
5. Why dimensional methods are applicable only up to three quantities?
Answers:
If a quantity depends on more than three factors than dimensional formula cannot be derived. Because on equating the powers of M, L & T on either side of the dimensional equation three equations can be obtained, from which only three unknown dimensions can be calculated
SOLVED EXAMPLE
1. Find the dimensions of a and b in the formula [P+ a/V2][V-b]=RT where P is pressure and V is the volume of the gas
Solution:
By the principle of homogeneity, a / V2 is of the dimensions of pressure and b is of the dimensions of volume.
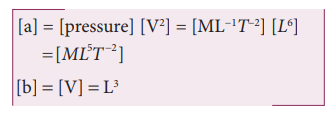
2. Show that (P-5/6 ρ1/2 E1/3 ) is of the dimension of time. Here P is the pressure, is the density and E is the energy of a bubble)
Solution:
Dimension of Pressure = [ML-1 T -2]
Dimension of density = [ML-3 ]
Dimension of Energy = [ML2 T -2 ]
By substituting in the given equation,
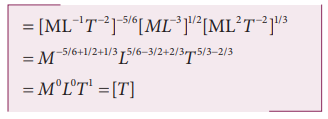
3. Find the dimensions of mass in terms of Energy, length and time
Solution:
Let the dimensions of Energy, Length and Time be [E ],[L],[T] respectively.
We know that Force = mass x acceleration
4. A physical quantity Q is found to depend on quantities x,y,z obeying relation Q =x1y3/z1. The percentage errors in x, y and z are 2%, 3% and 1% respectively. Find the percentage error in Q.
Solution:
5. The mass and volume of a body are found to be 4±.03 kg and 5±.01 m3 respectively. Then find the maximum possible percentage error in density.
Solution:
Error in density = error in mass + error in volume
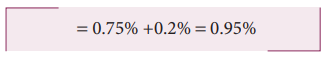
6. Using a Vernier Callipers, the length of a cylinder in different measurements is found to be 2.36 cm, 2.27 cm, 2.26 cm, 2.28 cm, 2.31 cm, 2.28 cm and 2.29 cm. Find the mean value, absolute error, the relative error and the percentage error of the cylinder.
Solution:
The given readings are 2.36 cm, 2.27 cm, 2.26 cm, 2.28 cm, 2.31 cm, 2.28 cm and 2.29 cm
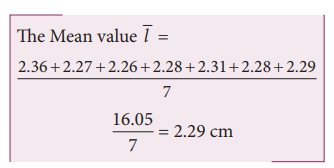
Absolute errors in the measurement are,
7. The shadow of a pole standing on a level ground is found to be 45 m longer when the sun’s altitude is 30° than when it was 60°. Determine the height of the pole. [Given √3 = 1.73]
Solution:
Let the height of the pole be h.
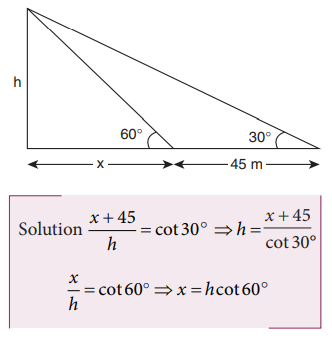
Substituting the values of x in the above equation
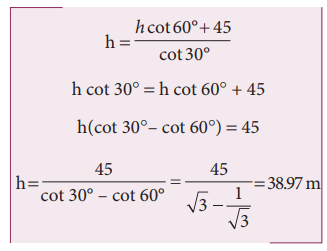
8. Calculate the number of times a human heart beats in the life of 100 years old man. Time of one heart beat = 0.8s.
Solution:
Life of the man = 100 years
100 years includes 76 normal years and 24 leap years
Total no of days = 76 × 365 + 24 × 366 = 36524 days
Number of seconds = 36524 × 24 × 3600 = 3.155 x 109 second
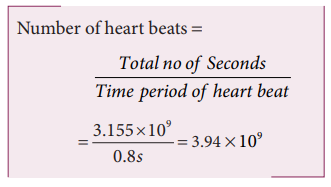
9. The parallax of a heavenly body measured from two points diametrically opposite on equator of earth is 2′. Calculate the distance of the heavenly body. [Given radius of the earth = 6400km] [1″ = 4.85 10-6 rad]
Solution:
Angle θ = 21 = 2 x 60″ = 120″ = 120 × 4.85 × 10-6 rad
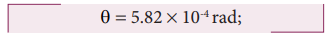
The distance of heavenly body
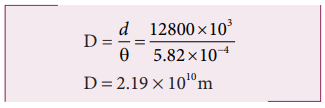
10. Convert a velocity of 72 kmh-1 into ms-1 with the help of dimensional analysis.
Solution:
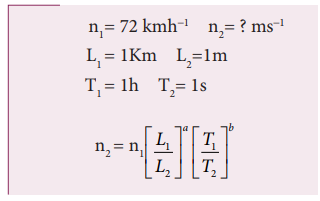
The dimensional formula for velocity is [L T-1]
11. Check the correctness of the following equation using dimensional analysis. Make a comment on it.
S = ut + 1/4 at2 where s is the displacement, u is the initial velocity, t is the time and a is the acceleration produced.
Solution:
Dimension for distance s = [L]
Dimension for initial velocity
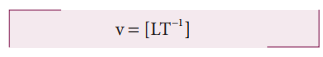
Dimension for time t = [T]
Dimension for acceleration
According to the principle of homogeneity,
Dimensions of LHS = Dimensions of RHS
Substituting the dimensions in the given formula
S = ut + 1/4 at2 1/4 is a number. It has no dimensions
As the dimensional formula of LHS is same as that of RHS, the equation is dimensionally correct.
Comment:
But actually it is a wrong equation. We know that the equation of motion is
So, a dimensionally correct equation need not be the true (or) actual equation S = ut + 1/4 at2
But a true equation is always dimensionally correct.
12. Round - off the following numbers as indicated.
a) 17.234 to 3 digits
b) 3.996 × 105 to 3 digits
c) 3.6925 × 10-3 to 2 digits
d) 124783 to 5 digits.
Solution:
a) 17.2
b) 4.00 × 105
c) 3.7 × 10-3
d) 124780
13. Solve the following with regard to significant figures.
a) √(4.5-3.31)
b) 5.9 × 105 - 2 .3 × 104
c) 7.18 + 4.3
d) 6.5 + .0136
Solution:
a) Among the two, the least number of significant after decimal is one
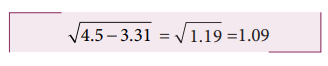
b) The number of minimum significant figures is 2
c) The lowest least number of significant digit after decimal is one
7.18 + 4.3 = 11.48 Rounding off we get 11.5
The lowest least number of significant digit after decimal is one
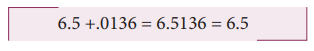
14. Arrive at Einstein’s mass-energy relation by dimensional method (E = mc2)
Solution:
Let us assume that the Energy E depends on mass m and velocity of light c.
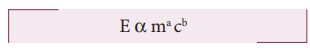
E =kma cb where K a constant
Dimensions of E = [ML2T -2 ]
Dimensions of m = [M]
Dimensions of c = [LT-1]
Substituting the values in the above equation
The value of constant k = 1
E = mc2 This is Einstein’s mass energy relation
15. The velocity of a body is given by the equation v = b/t + c t2+dt3. Find the dimensional formula for b.
Solution:
(b/t) should have the dimensions of velocity
b has the dimensions of (velocity time)
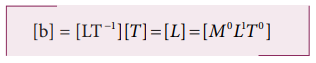
16. The initial and final temperatures of liquid in a container are observed to be 75.4 ± 0.5°C and 56.8 ± 0.2°C. Find the fall in the temperature of the liquid.
Solution:
t1 = (75.4 ± 0.5)°C
t2 = (56.8 ± 0.2)°C
Fall in temperature = (75.4 ± 0.5°C) – (56.8 ± 0.2°C)
17. Two resistors of resistances R1 = 150 ± 2 Ohm and R2 = 220 ± 6 Ohm are connected in parallel combination. Calculate the equivalent resistance.
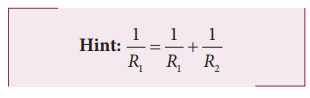
Solution:
The equivalent resistance of a parallel combination
Substituting the value,
18. A capacitor of capacitance C = 3.0 ± 0.1 µF is charged to a voltage of V = 18 ± 0.4Volt . Calculate the charge Q [Use Q= CV]
Solution:
(C + ∆C) = (3.0 ± 0.1) µf
(V + ∆V) = (18 ± 0.4) V
Q = CV
Solved Example Problems for Nature of Physical World and Measurement
Example 1.1
From a point on the ground, the top of a tree is seen to have an angle of elevation 60°. The distance between the tree and a point is 50 m. Calculate the height of the tree?
Solution
Angle θ = 60°
The distance between the tree and a point x = 50 m
Height of the tree (h) = ?
For triangulation method tan
h = x tan θ
= 50 × tan 60°
= 50 × 1.732
h = 86.6 m
The height of the tree is 86.6 m.
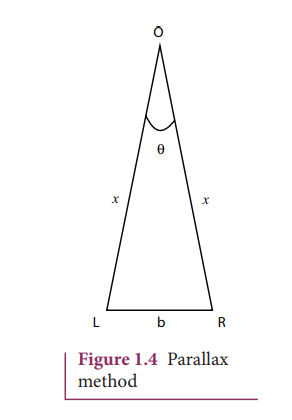
Parallax method
Very large distances, such as the distance of a planet or a star from the Earth can be measured by the parallax method. Parallax is the name given to the apparent change in the position of an object with respect to the background, when the object is seen from two different positions. The distance between the two positions (i.e., points of observation) is called the basis (b). For example, consider Figure 1.4., an observer is specified by the position O. The observer is holding a pen before him, against the background of a wall. When the pen is looked at first by our left eye L (closing the right eye) and then by our right eye R (closing the left eye), the position of the pen changes with respect to the back ground of the wall. The shift in the position of an object (say, a pen) when viewed with two eyes, keeping one eye closed at a time is known as Parallax. The distance between the left eye (L) and the right eye (R) in this case is the basis.
∠LOR is called the parallax angle or parallactic angle.
Taking LR as an arc of length b and radius LO = RO = x
we get θ = b/x, b-basis, x-unknown distance
Knowing ‘b’ and measuring θ, we can calculate x.
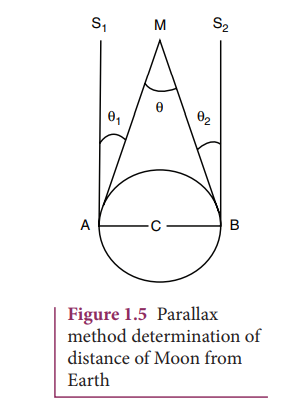
Determination of distance of Moon from Earth
In Figure 1.5, C is the centre of the Earth. A and B are two diametrically opposite places on the surface of the Earth. From A and B, the parallaxes θ1 and θ2 respectively of Moon M with respect to some distant star are determined with the help of an astronomical telescope. Thus, the total parallax of the Moon subtended on Earth ∠AMB = θ1 + θ2 = θ.
If θ is measured in radians, then
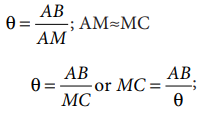
Knowing the values of AB and θ,
we can calculate the distance MC of Moon from the Earth.
Example 1.2
The Moon subtends an angle of 1° 55’ at the base line equal to the diameter of the Earth. What is the distance of the Moon from the Earth? (Radius of the Earth is 6.4 × 106 m)
Solution
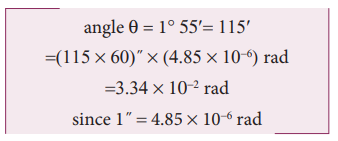
Radius of the Earth = 6.4 × 106 m
From the Figure 1.5 AB is the diameter of the Earth (b)= 2 × 6.4 × 106 m Distance of the Moon from the Earth x = ?
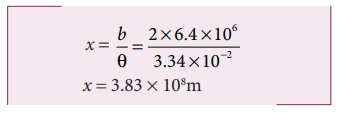
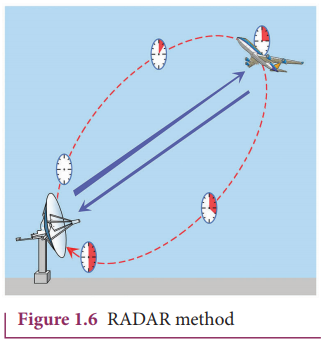
RADAR method
The word RADAR stands for radio detection and ranging. A radar can be used to measure accurately the distance of a nearby planet such as Mars. In this method, radio waves are sent from transmitters which, after reflection from the planet, are detected by the receiver. By measuring, the time interval (t) between the instants the radio waves are sent and received, the distance of the planet can be determined as
where v is the speed of the radio wave. As the time taken (t) is for the distance covered during the forward and backward path of the radio waves, it is divided by 2 to get the actual distance of the object. This method can also be used to determine the height, at which an aeroplane flies from the ground.
Example 1.3
A RADAR signal is beamed towards a planet and its echo is received 7 minutes later. If the distance between the planet and the Earth is 6.3 × 1010 m. Calculate the speed of the signal?
Solution
The distance of the planet from the Earth d = 6.3 × 1010 m
The speed of signal
Example 1.4
In a series of successive measurements in an experiment, the readings of the period of oscillation of a simple pendulum were found to be 2.63s, 2.56 s, 2.42s, 2.71s and 2.80s. Calculate (i) the mean value of the period of oscillation (ii) the absolute error in each measurement (iii) the mean absolute error (iv) the relative error (v) the percentage error. Express the result in proper form.
Solution
Example 1.5
Two resistances R1 = (100 ± 3) Ω, R2 = (150 ± 2) Ω, are connected in series. What is their equivalent resistance?
Solution
Equivalent resistance R = ?
Equivalent resistance R = R1 + R2
Example 1.6
The temperatures of two bodies measured by a thermometer are t1 = (20 + 0.5)°C, t2 = (50 ± 0.5)°C. Calculate the temperature difference and the error therein.
Solution
Example 1.7
The length and breadth of a rectangle are (5.7 ± 0.1) cm and (3.4 ± 0.2) cm respectively. Calculate the area of the rectangle with error limits.
Solution
Example 1.8
The voltage across a wire is (100 ± 5)V and the current passing through it is (10±0.2) A. Find the resistance of the wire.
Solution
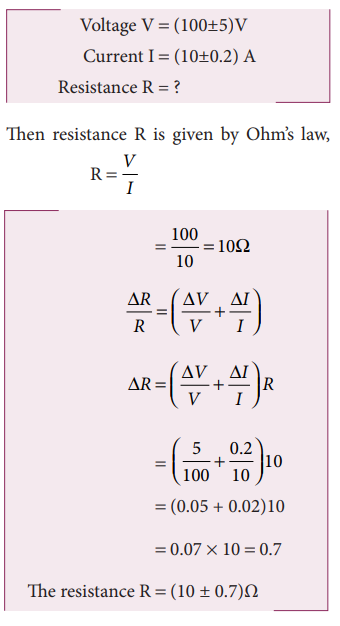
Example 1.9
A physical quantity x is given by x
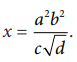
If the percentage errors of measurement in a, b, c and d are 4%, 2%, 3% and 1% respectively then calculate the percentage error in the calculation of x.
Solution
The percentage error in x is given by
The percentage error is x = 17.5%
Example 1.10
State the number of significant figures in the following
i. 600800
ii. 400
iii. 0.007
iv. 5213.0x
v. 2.65 × 1024 m
vi. 0.0006032
Solution
Solution: i) four ii) one iii) one iv) five v) three vi) four
Example 1.11
Round off the following numbers as indicated
i) 18.35 up to 3 digits
ii) 19.45 up to 3 digits
iii) 101.55 × 106 up to 4 digits
iv) 248337 up to digits 3 digits
v) 12.653 up to 3 digits.
Solution
i) 18.4 ii) 19.4 iii) 101.6 × 106 iv) 248000 v) 12.7
Example 1.12
Convert 76 cm of mercury pressure into Nm−2 using the method of dimensions.
Solution
In cgs system 76 cm of mercury pressure = 76 × 13.6 × 980 dyne cm−2
The dimensional formula of pressure P is [ML−1T−2]
Example 1.13
If the value of universal gravitational constant in SI is 6.6x10−11 Nm2 kg−2, then find its value in CGS System?
Solution
Let GSI be the gravitational constant in the SI system and Gcgs in the cgs system. Then
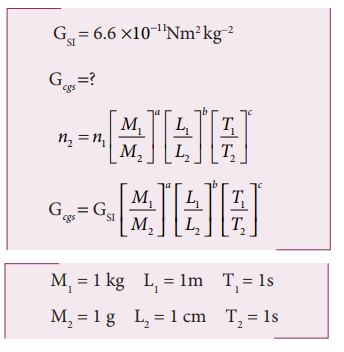
The dimensional formula for G is M−1 L3T −2
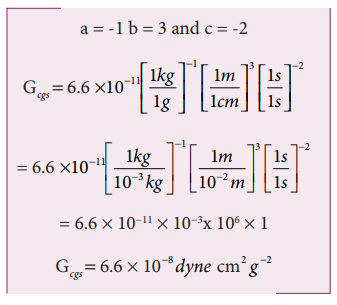
Example 1.14
Check the correctness of the equation
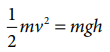
using dimensional analysis method
Solution
Both sides are dimensionally the same, hence the equations
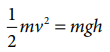
is dimensionally correct.
Example 1.15
Obtain an expression for the time period T of a simple pendulum. The time period T depends on (i) mass ‘m’ of the bob (ii) length ‘l’ of the pendulum and (iii) acceleration due to gravity g at the place where the pendulum is suspended. (Constant k = 2π) i.e
Solution
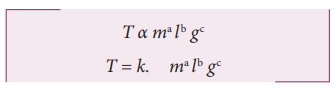
Here k is the dimensionless constant. Rewriting the above equation with dimensions
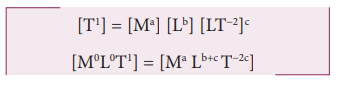
Comparing the powers of M, L and T on both sides, a=0, b+c=0, -2c=1
Solving for a,b and c a = 0, b = 1/2, and c = −1/2
From the above equation T = k. m0 l1/2 g−1/2
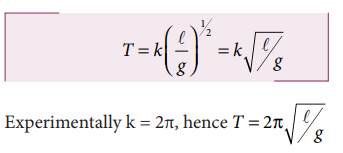
Example 1.16
The force F acting on a body moving in a circular path depends on mass of the body (m), velocity (v) and radius (r) of the circular path. Obtain the expression for the force by dimensional analysis method. (Take the value of k=1)
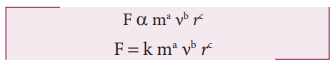
where k is a dimensionless constant of proportionality. Rewriting above equation in terms of dimensions and taking k = 1, we have
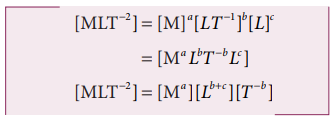
Comparing the powers of M, L and T on both sides
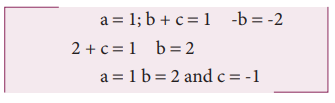
From the above equation we get
Related Topics