with Solved Example Problems - Measurement of length | 11th Physics : UNIT 1 : Nature of Physical World and Measurement
Chapter: 11th Physics : UNIT 1 : Nature of Physical World and Measurement
Measurement of length
Measurement of length
The concept of length in physics is related to the concept of distance in everyday life. Length is defined as the distance between any two points in space. The SI unit of length is metre. The objects of our interest vary widely in sizes. For example, large objects like the galaxy, stars, Sun, Earth, Moon etc., and their distances constitute a macrocosm. It refers to a large world, in which both objects and distances are large. On the contrary, objects like molecules, atoms, proton, neutron, electron, bacteria etc., and their distances constitute microcosm, which means a small world in which both objects and distances are small-sized.
The Radian (rad): One radian is the angle subtended at the centre of a circle by an arc equal in length to the radius of the circle.
The Steradian (sr): One steradian is the solid angle subtended at the centre of a sphere, by that surface of the sphere, which is equal in area, to the square of radius of the sphere
Distances ranging from 10−5 m to 102m can be measured by direct methods. For example, a metre scale can be used to measure the distance from 10−3 m to 1 m, vernier calipers up to 10−4m, a screw gauge up to 10−5 m and so on. The atomic and astronomical distances cannot be measured by any of the above mentioned direct methods. Hence, to measure the very small and the very large distances, indirect methods have to be devised and used. In Table 1.4, a list of powers of 10 (both positive and negative powers) is given. Prefixes for each power are also mentioned. These prefixes are used along with units of length, and of mass.
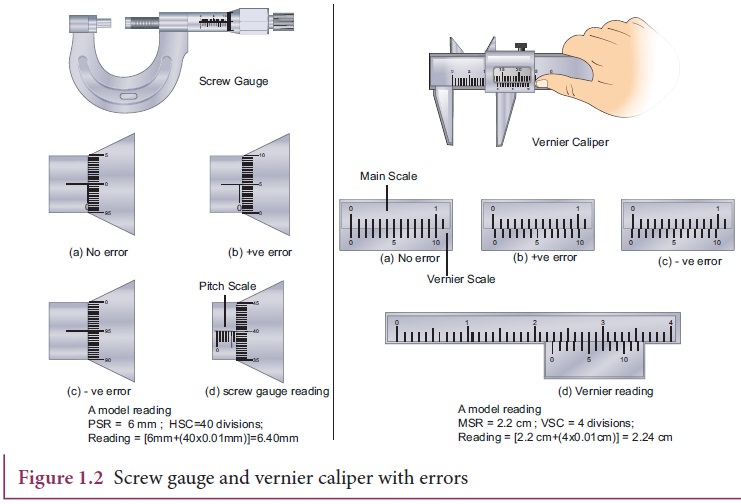
i. Measurement of small distances: screw gauge and vernier caliper Screw gauge:
The screw gauge is an instrument used for measuring accurately the dimensions of objects up to a maximum of about 50 mm. The principle of the instrument is the magnification of linear motion using the circular motion of a screw. The least count of the screw gauge is 0.01 mm Vernier caliper: A vernier caliper is a versatile instrument for measuring the dimensions of an object namely diameter of a hole, or a depth of a hole. The least count of the vernier caliper is 0.1 mm
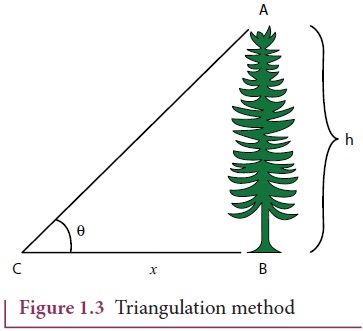
ii. Measurement of large distances
For measuring larger distances such as the height of a tree, distance of the Moon or a planet from the Earth, some special methods are adopted. Triangulation method, parallax method and radar method are used to determine very large distances.
Triangulation method for the height of an accessible object
Let AB = h be the height of the tree or tower to be measured. Let C be the point of observation at distance x from B. Place a range finder at C and measure the angle of elevation, ∠ACB = θ as shown in Figure 1.3.

height h = x tan θ
Knowing the distance x, the height h can be determined.
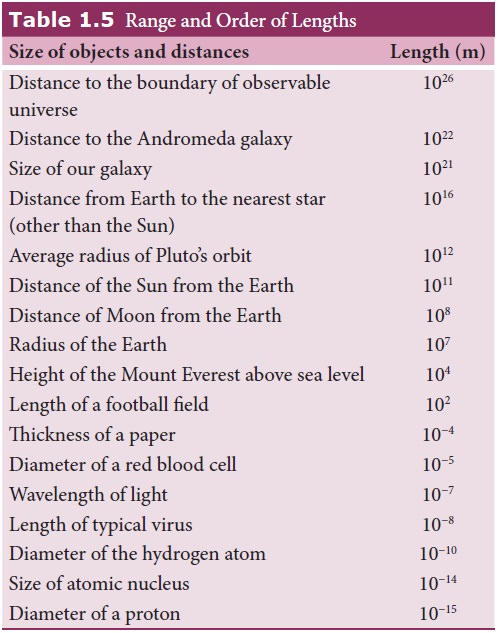
Range and order of lengths of various objects are listed in Table 1.5

Solved Example Problems for Measurement of length
Example 1.1
From a point on the ground, the top of a tree is seen to have an angle of elevation 60°. The distance between the tree and a point is 50 m. Calculate the height of the tree?
Solution
Angle θ = 60°
The distance between the tree and a point x = 50 m
Height of the tree (h) = ?
For triangulation method tan
h = x tan θ
= 50 × tan 60°
= 50 × 1.732
h = 86.6 m

The height of the tree is 86.6 m.
Parallax method
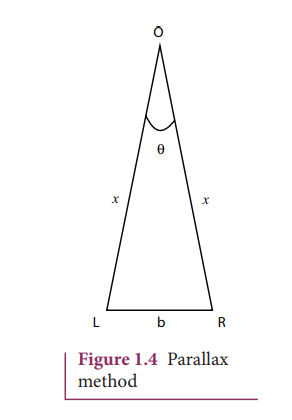
Very large distances, such as the distance of a planet or a star from the Earth can be measured by the parallax method. Parallax is the name given to the apparent change in the position of an object with respect to the background, when the object is seen from two different positions. The distance between the two positions (i.e., points of observation) is called the basis (b). For example, consider Figure 1.4., an observer is specified by the position O. The observer is holding a pen before him, against the background of a wall. When the pen is looked at first by our left eye L (closing the right eye) and then by our right eye R (closing the left eye), the position of the pen changes with respect to the back ground of the wall. The shift in the position of an object (say, a pen) when viewed with two eyes, keeping one eye closed at a time is known as Parallax. The distance between the left eye (L) and the right eye (R) in this case is the basis.
∠LOR is called the parallax angle or parallactic angle.
Taking LR as an arc of length b and radius LO = RO = x
we get θ = b/x, b-basis, x-unknown distance
Knowing ‘b’ and measuring θ, we can calculate x.
Determination of distance of Moon from Earth
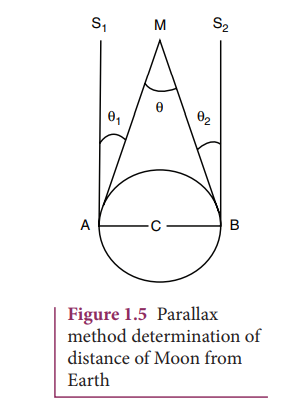
In Figure 1.5, C is the centre of the Earth. A and B are two diametrically opposite places on the surface of the Earth. From A and B, the parallaxes θ1 and θ2 respectively of Moon M with respect to some distant star are determined with the help of an astronomical telescope. Thus, the total parallax of the Moon subtended on Earth ∠AMB = θ1 + θ2 = θ.
If θ is measured in radians, then
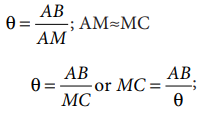
Knowing the values of AB and θ,
we can calculate the distance MC of Moon from the Earth.
Example 1.2
The Moon subtends an angle of 1° 55’ at the base line equal to the diameter of the Earth. What is the distance of the Moon from the Earth? (Radius of the Earth is 6.4 × 106 m)
Solution
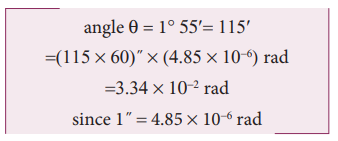
Radius of the Earth = 6.4 × 106 m
From the Figure 1.5 AB is the diameter of the Earth (b)= 2 × 6.4 × 106 m Distance of the Moon from the Earth x = ?
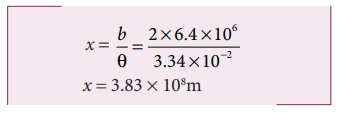
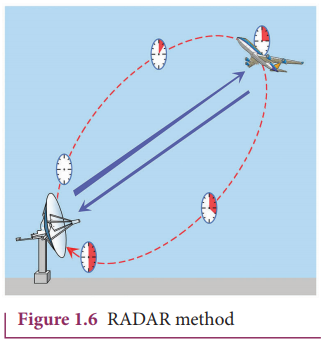
RADAR method
The word RADAR stands for radio detection and ranging. A radar can be used to measure accurately the distance of a nearby planet such as Mars. In this method, radio waves are sent from transmitters which, after reflection from the planet, are detected by the receiver. By measuring, the time interval (t) between the instants the radio waves are sent and received, the distance of the planet can be determined as

where v is the speed of the radio wave. As the time taken (t) is for the distance covered during the forward and backward path of the radio waves, it is divided by 2 to get the actual distance of the object. This method can also be used to determine the height, at which an aeroplane flies from the ground.
Example 1.3
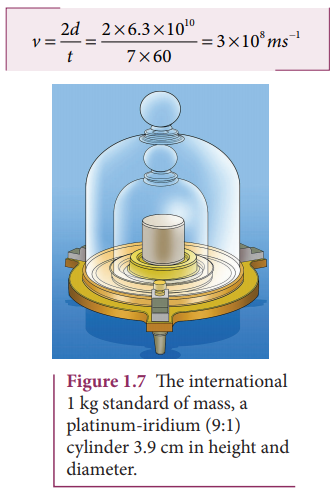
A RADAR signal is beamed towards a planet and its echo is received 7 minutes later. If the distance between the planet and the Earth is 6.3 × 1010 m. Calculate the speed of the signal?
Solution
The distance of the planet from the Earth d = 6.3 × 1010 m

The speed of signal
Related Topics