Absolute, Mean Absolute, Relative, Percentage error | Theory of Errors | Physics - Error Analysis | 11th Physics : UNIT 1 : Nature of Physical World and Measurement
Chapter: 11th Physics : UNIT 1 : Nature of Physical World and Measurement
Error Analysis
Error
Analysis
i. Absolute Error
The
difference between the true value and the measured value of a quantity is
called absolute error. If a1, a2, a3, ………. an are the measured values of any quantity ‘a’ in an experiment performed n
times, then the arithmetic mean of these
values is called the true value (am)
of the quantity.
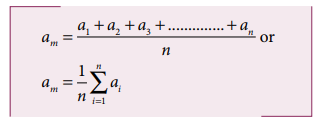
The
absolute error in measured values is given by
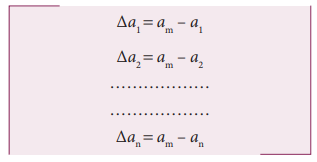
ii. Mean Absolute error
The
arithmetic mean of the magnitude of absolute errors in all the measurements is
called the mean absolute error.
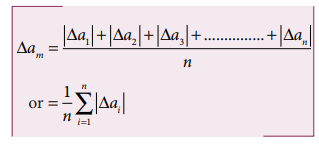
If
am is the true value and ∆am is the mean absolute error then the
magnitude of the quantity may lie between am
+ ∆am and am - ∆am
iii. Relative error
The
ratio of the mean absolute error to the mean value is called relative error.
This is also called as fractional error (or) relative error.

Thus Relative
error expresses how large the absolute error is compared to the total size of
the object measured. For example, a driver’s speedometer shows that his car is
travelling at 60 km h-1 when it is actually moving at 62 kmh-1.
Then absolute error of speedometer is 62-60 km h-1 = 2 km h-1
Relative error of the measurement is 2 km h-1 / 60 km h-1
= 0.033.
iv. Percentage error
The
relative error expressed as a percentage is called percentage error.

A
percentage error very close to zero means one is close to the targeted value,
which is good and acceptable. It is always necessary to understand whether
error is due to impression of equipment used or a mistake in the
experimentation.
Example 1.4
In a series of successive measurements in an experiment, the readings of the period of oscillation of a simple pendulum were found to be 2.63s, 2.56 s, 2.42s, 2.71s and 2.80s. Calculate (i) the mean value of the period of oscillation (ii) the absolute error in each measurement (iii) the mean absolute error (iv) the relative error (v) the percentage error. Express the result in proper form.
Solution


Related Topics