with Answers, Solution | Dual Nature of Radiation and Matter | Physics - Solved Example Numerical problems | 12th Physics : UNIT 8 : Dual Nature of Radiation and Matter
Chapter: 12th Physics : UNIT 8 : Dual Nature of Radiation and Matter
Solved Example Numerical problems
Concept of quantization of energy - Numerical Problems Questions with Answers, Solution
EXAMPLE 7.1
For the photoelectric emission from cesium, show that wave theory predicts that
i) maximum kinetic energy of the photoelectrons (Kmax) depends on the intensity I of the incident light
ii) Kmax does not depend on the frequency of the incident light and
iii) the time interval between the incidence of light and the ejection of photoelectrons is very long.
(Given : The work function for cesium is 2.14 eV and the power absorbed per unit area is 1.60├Ś10ŌłÆ6WmŌłÆ2 which produces a measurable photocurrent in cesium.)
Solution
i) According to wave theory, the energy in a light wave is spread out uniformly and continuously over the wavefront. For the sake of simplicity, the following assumptions are made.
a) Light is absorbed in the top atomic layer of the metal
b) For a given element, each atom absorbs an equal amount of energy and this energy is proportional to its cross-sectional area A
c) Each atom gives this energy to one of the electrons.
The energy absorbed by each electron in time t is given by
E = IAt
With this energy absorbed, the most energetic electron is released with Kmax by overcoming the surface energy barrier or work function ŽĢ0 and this is expressed as
Kmax = IAt ŌłÆ ŽĢ0 (1)

Thus, wave theory predicts that for a unit time, at low light intensities when IA < ŽĢ0, no electrons are emitted. At higher intensities, when IA Ōēź ŽĢ0, electrons are emitted. This implies that higher the light intensity, greater will be Kmax.
Therefore, the predictions of wave theory contradict experimental observations at both very low and very high light intensities.
Kmax is dependent only on the intensity under given conditions ŌĆō that is, by suitably increasing the intensity, one can produce photoelectric effect even if the frequency is less than the threshold frequency. So the concept of threshold frequency does not even exist in wave theory.
ii) According to wave theory, the intensity of a light wave is proportional to the square of the amplitude of the electric field (E02). The amplitude of this electric field increases with increasing intensity and imparts an increasing acceleration and kinetic energy to an electron.
Now I is replaced with a quantity proportional to E2 in equation (1). This means that Kmax should not depend at all on the frequency of the classical light wave which again contradicts the experimental results.
iii) If an electron accumulates light energy just enough to overcome the work function, then it is ejected out of the atom with zero kinetic energy. Therefore, from equation (1),
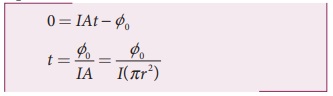
By taking the atomic radius r = 1.0├Ś10ŌłÆ10 m and substituting the given values of I and ŽĢ0, we can estimate the time interval as
t = 2.14├Ś1.6├Ś10ŌłÆ19 / 1.60├Ś10ŌłÆ6 ├Ś3.14├Ś(1├Ś10ŌłÆ10)2
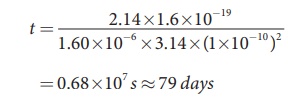
= 0.68├Ś107 s Ōēł 79 days
Thus, wave theory predicts that there is a large time gap between the incidence of light and the ejection of photoelectrons but the experiments show that photo emission is an instantaneous process.
Photo Electric Effect - Numerical Problems Questions with Answers, Solution
EXAMPLE 7.2
A radiationof wavelength 300 nm is incident on a silver surface. Will photoelectrons be observed?
Solution:
Energy of the incident photon is
E = hv = hc/╬╗ (in joules)
E = hc/╬╗e (in eV)
Substituting the known values, we get
E = 6.626├Ś10ŌłÆ34 ├Ś3├Ś108 / 300├Ś10ŌłÆ9 ├Ś1.6├Ś10ŌłÆ19
E = 4.14 eV
From Table 7.1, the work function of silver = 4.7 eV. Since the energy of the incident photon is less than the work function of silver, photoelectrons are not observed in this case.
EXAMPLE 7.3
When light of wavelength 2200├ģ falls on Cu, photo electrons are emitted from it. Find (i) the threshold wavelength and (ii) the stopping potential. Given: the work function for Cu is ŽĢ0 = 4.65 eV.
Solution
i) The threshold wavelength is given by
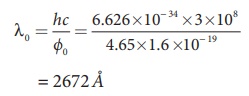
= 2672 ├ģ
ii) Energy of the photon of wavelength 2200 ├ģ is
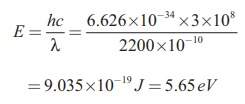
= 9.035├Ś10ŌłÆ19 J = 5.65 eV
We know that kinetic energy of fastest photo electron is
Kmax = hv ŌĆō ŽĢ0 = 5.65 ŌĆō 4.65
= 1 eV
From equation (7.3), Kmax = eV0
V0 = Kmax/e 1├Ś1.6├Ś10ŌłÆ19 / 1.6├Ś10ŌłÆ19
Therefore, stopping potential = 1V
EXAMPLE 7.4
The work function of potassium is 2.30 eV. UV light of wavelength 3000 ├ģ and intensity 2 Wm-2 is incident on the potassium surface. i) Determine the maximum kinetic energy of the photo electrons ii) If 40% of incident photons produce photo electrons, how many electrons are emitted per second if the area of the potassium surface is 2 cm2 ?
Solution
i) The energy of the photon is
E = hc/╬╗
= 6.626├Ś10ŌłÆ34 ├Ś 3├Ś108 / 3000├Ś10ŌłÆ10
E = 6.626├Ś10ŌłÆ19 J = 4.14 eV
Maximum KE of the photoelectrons is
Kmax = hv ŌĆō ŽĢ0 = 4.14 ŌĆō 2.30 = 1.84 eV
ii) The number of photons reaching the surface per second is
np = P/E ├Ś A
= [ 2 / 6.626├Ś10ŌłÆ19 ] ├Ś [2├Ś10ŌłÆ4]
= 6.04├Ś1014 photons / sec
The rate of emission of photoelectrons is
= (0.40)np = 0.4├Ś6.04├Ś1014
= 2.415┬┤1014 photoelectrons / sec
EXAMPLE 7.5
Light of wavelength 390 nm is directed at a metal electrode. To find the energy of electrons ejected, an opposing potential difference is established between it and another electrode. The current of photoelectrons from one to the other is stopped completely when the potential difference is 1.10 V. Determine i) the work function of the metal and ii) the maximum wavelength of light that can eject electrons from this metal.
Solution
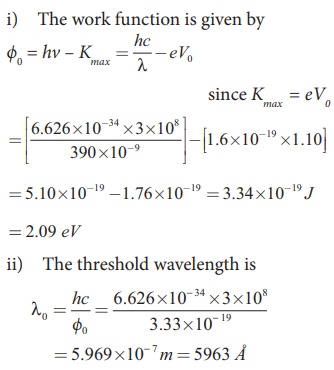
Wave nature of particles - Numerical Problems Questions with Answers, Solution
EXAMPLE 7.6
Calculate the momentum and the de Broglie wavelength in the following cases:
i) an electron with kinetic energy 2 eV.
ii) a bullet of 50 g fired from rifle with a speed of 200 m/s
iii) a 4000 kg car moving along the highways at 50 m/s
Hence show that the wave nature of matter is important at the atomic level but is not really relevant at macroscopic level.
Solution:

From these calculations, we notice that electron has significant value of de Broglie wavelength (Ōēł10ŌĆō9m which can be measured from difraction studies) but bullet and car have negligibly small de Broglie wavelengths associated with them (Ōēł10ŌĆō33m and 10ŌĆō39m respectively, which are not measurable by any experiment). This implies that the wave nature of matter is important at the atomic level but it is not really relevant at the macroscopic level.
EXAMPLE 7.7
Find the de Broglie wavelength associated with an alpha particle which is accelerated through a potential difference of 400 V. Given that the mass of the proton is 1.67 ├Ś 10ŌĆō27 kg.
Solution
An alpha particle contains 2 protons and 2 neutrons. Therefore, the mass M of the alpha particle is 4 times that of a proton (mp) (or a neutron) and its charge q is twice that of a proton (+e).
The de Broglie wavelength associated with it is
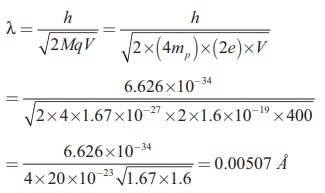
EXAMPLE 7.8
A proton and an electron have same de Broglie wavelength. Which of them moves faster and which possesses more kinetic energy?
Solution
We know that ╬╗ = h/ ŌłÜ(2mK)
Since proton and electron have same de Broglie wavelength, we get
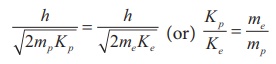
Since me < mp , Kp < Ke , the electron has more kinetic energy than the proton.
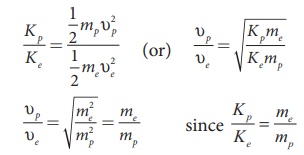
Since me < mp , Žģp < Žģe , the electron moves faster than the proton.
X-Rays - Numerical Problems Questions with Answers, Solution
EXAMPLE 7.9
Calculate the cut-off wavelength and cut- off frequency of x-rays from an x ŌĆōray tube of accelerating potential 20,000 V.
Solution
The cut-off wavelength of the characteristic x-rays is

= 0.62 ├ģ
The corresponding frequency is
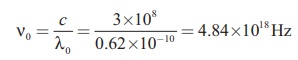
IV Numerical problems
1. How many photons per second emanate from a 50 mW laser of 640 nm?
[Ans:1.61├Ś1017 sŌłÆ1 ]

2. Calculate the maximum kinetic energy and maximum velocity of the photoelectrons emitted when the stopping potential is 81V for the photoelectric emission experiment.
[[Ans: 1.3├Ś10ŌĆō17J; 5.3├Ś106 msŌĆō1]]

3. Calculate the energies of the photons associated with the following radiation: (i) violet light of 413 nm (ii) X-rays of 0.1 nm (iii) radio waves of 10 m.
[Ans: 3eV ; 12424eV ;1.24├Ś10ŌłÆ7 eV ]
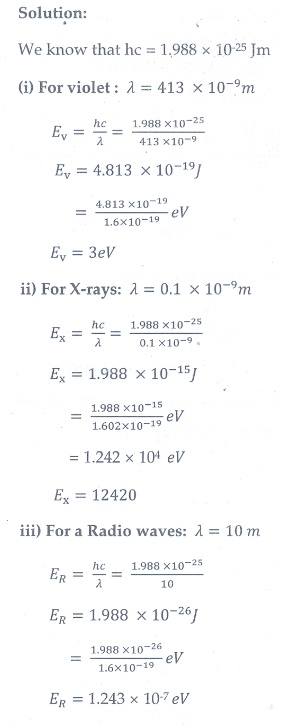
4. A 150 W lamp emits light of mean wavelength of 5500 ├ģ . If the efficiency is 12%, find out the number of photons emitted by the lamp in one second.
[Ans: 4.98├Ś1019 ]

5. How many photons of frequency 1014 Hz will make up 19.86 J of energy?
[Ans: 3┬┤1020 ]

6. What should be the velocity of the electron so that its momentum equals that of 4000 ├ģ wavelength photon.
[Ans: 1818ms-1 ]

7. When a light of frequency 9┬┤1014 Hz is incidentona metal surface, photoelectrons are emitted with a maximum speed of 8├Ś105 msŌłÆ1 . Determine the threshold frequency of the surface.
[Ans: 4.61┬┤1014 Hz ]

8. When a 6000 ├ģ light falls on the cathode of a photo cell and produced photoemission. If a stopping potential of 0.8 V is required to stop emission of electron, then determine the (i) frequency of the light (ii) energy of the incident photon (iii) work function of the cathode material (iv) threshold frequency and (v) net energy of the electron after it leaves the surface.
[Ans: 5├Ś1014 Hz; 2.07 eV; 1.27 eV; 3.07├Ś1014 Hz; 0.8 eV ]

9. A 3310 ├ģ photon liberates an electron from a material with energy 3├Ś10ŌłÆ19 J while another 5000 ├ģ photon ejects an electron with energy 0.972├Ś10ŌłÆ19 J from the same material. Determine the value of PlanckŌĆÖs constant and the threshold wavelength of the material.
[Ans: 6.62├Ś10ŌłÆ34 Js; 6620├Ś10ŌłÆ10 m ]

10. At the given point of time, the earth receives energy from sun at 4 cal cm-2 min-1. Determine the number of photons received on the surface of the Earth per cm2 per minute. (Given : Mean wavelength of sun light = 5500 ├ģ )
[Ans: 4.65┬┤1019 ]

11. UV light of wavelength 1800 ├ģ is incident on a lithium surface whose threshold wavelength 4965 ├ģ . Determine the maximum energy of the electron emitted.
[Ans: 4.40 eV]

12. Calculate the de Broglie wavelength of a proton whose kinetic energy is equal to 81.9 ├Ś 10ŌĆō15 J. (Given: mass of proton is 1836 times that of electron).
[Ans: 4├Ś10ŌłÆ14 m ]
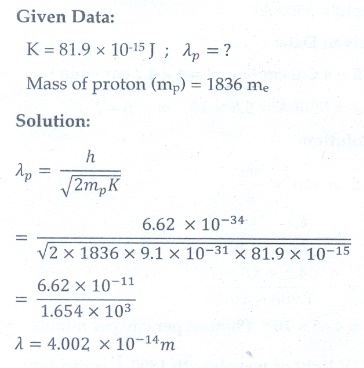
13. A deuteron and an alpha particle are accelerated with the same potential. Which one of the two has i) greater value of de Broglie wavelength associated with it and ii) less kinetic energy? Explain.
[Ans: ╬╗d = 2╬╗╬▒ and Kd = Kd= Kd/2 ]

14. An electron is accelerated through a potential difference of 81V. What is the de Broglie wavelength associated with it? To which part of electromagnetic spectrum does this wavelength correspond?
[Ans: ╬╗ =1.36 ├ģ and x-rays]
15. The ratio between the de Broglie wavelengths associated with protons, accelerated through a potential of 512 V and that of alpha particles accelerated through a potential of X volts is found to be one. Find the value of X.
[Ans: 64 V]

Related Topics