Photo Electric Effect | Physics - Concept of quantization of energy | 12th Physics : UNIT 8 : Dual Nature of Radiation and Matter
Chapter: 12th Physics : UNIT 8 : Dual Nature of Radiation and Matter
Concept of quantization of energy
PHOTO ELECTRIC EFFECT
Concept of quantization of energy
Failures of classical wave theory
From MaxwellŌĆÖs theory (Refer unit 5
of volume 1), we learnt that light is an electromagnetic wave consisting of
coupled electric and magnetic oscillations that move with the speed of light
and exhibit typical wave behaviour. Let us try to explain the experimental
observations of photoelectric effect using wave picture of light.
i) When light is incident on the
target, there is a continuous supply of energy to the electrons. According to
wave theory, light of greater intensity should impart greater kinetic energy to
the liberated electrons (Here, Intensity of light is the energy delivered per
unit area per unit time).
But this does not happen. The experiments
show that maximum kinetic energy of the photoelectrons does not depend on the
intensity of the incident light.
ii) According to
wave theory, if a sufficiently intense beam of light is incident on the
surface, electrons will be liberated from the surface of the target, however
low the frequency of the radiation is.
From the experiments, we know that
photoelectric emission is not possible below a certain minimum frequency.
Therefore, the wave theory fails to explain the existence of threshold
frequency.
iii) Since the energy of light is
spread across the wavefront, the electrons which receive energy from it are
large in number. Each electron needs considerable amount of time (a few hours)
to get energy sufficient to overcome the work function and to get liberated
from the surface.
But experiments show that
photoelectric emission is almost instantaneous process (the time lag is less
than 10ŌĆō9 s after the
surface is illuminated) which could not be explained by wave theory.
Thus, the experimental observations
of photoelectric emission could not be explained on the basis of the wave
theory of light.
EXAMPLE 7.1
For the photoelectric emission from
cesium, show that wave theory predicts that
i) maximum kinetic
energy of the photoelectrons (Kmax)
depends on the intensity I of the
incident light
ii) Kmax does not depend on the
frequency of the incident light and
iii) the time interval between the
incidence of light and the ejection of photoelectrons is very long.
(Given : The work function for
cesium is 2.14 eV and the power
absorbed per unit area is 1.60├Ś10ŌłÆ6WmŌłÆ2 which produces a measurable photocurrent in
cesium.)
Solution
i) According to
wave theory, the energy in a light wave is spread out uniformly and
continuously over the wavefront. For the sake of simplicity, the following
assumptions are made.
a) Light is
absorbed in the top atomic layer of the metal
b) For a given
element, each atom absorbs an equal amount of energy and this energy is
proportional to its cross-sectional area A
c) Each atom gives
this energy to one of the electrons.
The energy absorbed by each electron
in time t is given by
E = IAt
With this energy absorbed, the most
energetic electron is released with Kmax by overcoming the surface energy barrier or work function ŽĢ0 and this is expressed as
Kmax = IAt ŌłÆ ŽĢ0 (1)

Thus, wave theory predicts that for
a unit time, at low light intensities when IA < ŽĢ0, no electrons are emitted. At
higher intensities, when IA Ōēź ŽĢ0, electrons are emitted. This
implies that higher the light intensity, greater will be Kmax.
Therefore, the predictions of wave
theory contradict experimental observations at both very low and very high
light intensities.
Kmax is dependent only
on the intensity under given conditions ŌĆō that is, by suitably increasing the intensity, one can produce photoelectric
effect even if the frequency is less than the threshold frequency. So the
concept of threshold frequency does not even exist in wave theory.
ii) According to wave theory, the
intensity of a light wave is proportional to the square of the amplitude of the
electric field (E02). The amplitude of this electric
field increases with increasing intensity and imparts an increasing
acceleration and kinetic energy to an electron.
Now I is replaced with a quantity proportional to E2 in equation (1). This means that Kmax should not depend at all on the frequency of the
classical light wave which again contradicts the experimental results.
iii) If an electron accumulates
light energy just enough to overcome the work function, then it is ejected out
of the atom with zero kinetic energy. Therefore, from equation (1),
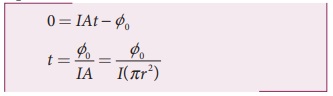
By taking the atomic radius r = 1.0├Ś10ŌłÆ10 m and substituting the given values of I and ŽĢ0, we can estimate the time interval as
t = 2.14├Ś1.6├Ś10ŌłÆ19 / 1.60├Ś10ŌłÆ6
├Ś3.14├Ś(1├Ś10ŌłÆ10)2
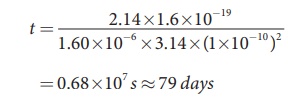
= 0.68├Ś107 s Ōēł 79 days
Thus, wave theory predicts that
there is a large time gap between the incidence of light and the ejection of
photoelectrons but the experiments show that photo emission is an instantaneous process.
Concept of quantization of energy
Max Planck proposed quantum concept in
1900 in order to explain the thermal radiations emitted by a black body and the
shape of its radiation curves.
According to Planck, matter is composed
of a large number of oscillating particles (atoms) which vibrate with different
frequencies. Each atomic oscillator - which vibrates with its characteristic
frequency - emits or absorbs electromagnetic radiation of the same frequency.
It also says that
i) If an oscillator
vibrates with frequency v, its energy
can have only certain discrete values, given by the equation.
En= nh╬Į n=1,2,3.... (7.4)
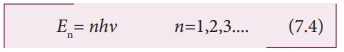
where h is a constant, called PlanckŌĆÖs constant.
ii) The oscillators emit or absorb
energy in small packets or quanta and the energy of each quantum is E = h╬Į.
This implies that the energy of the
oscillator is quantized ŌĆō that is, energy is not continuous as believed in the
wave picture. This is called quantization
of energy.
Related Topics