De Broglie wave length of electrons

De Broglie wave:

The wave–particle duality of radiation was extended to matter by a French physicist Louis de Broglie (pronounced as de Broy) in 1924.

Greatly influenced by the symmetry in nature, de Broglie suggested that if radiation like light can act as particles at times, then matter particles like electrons should also act as waves at times.

According to de Broglie hypothesis, all matter particles like electrons, protons, neutrons in motion are associated with waves. These waves are called de Broglie waves or matter waves.

De Broglie wave length:

The momentum of photon of frequency ν is given by

The wavelength of a photon in terms of its momentum is

According to de Broglie, the above equation is completely a general one and this is applicable to material particles as well. Therefore, for a particle of mass m travelling with speed Ï…, the wavelength is given by

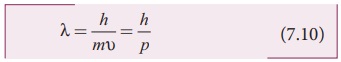
This wavelength of the matter waves is known as de Broglie wavelength. This equation relates the wave character (the wave length λ) and the particle character (the momentum p) through Planck’s constant.

De Broglie wave length of electrons:

An electron of mass m is accelerated through a potential difference of V volt. The kinetic energy acquired by the electron is given by

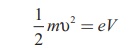
Therefore, the speed Ï… of the electron is

Hence, the de Broglie wavelength of the electron is

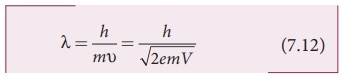
Substituting the known values in the above equation, we get

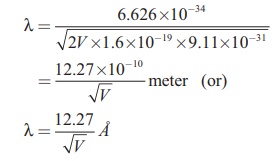
For example, if an electron is accelerated through a potential difference of 100V, then its de Broglie wavelength is 1.227 Ã….

Since the kinetic energy of the electron, K = eV, then the de Broglie wavelength associated with electron can be also written as