Ray Optics

RAY OPTICS

An age is called dark, not because the light fails to shine, but because people refuse to see.

-James Albert Michener

There are two ways of spreading light: to be the candle or the mirror that reflects it.

-Edith Wharton

LEARNING OBJECTIVES

In this unit, the students are exposed to,

• The ray aspect of light.

• The phenomenon of reflection and refraction of light.

• The determination of speed of light.

• The concepts related to mirrors, lenses, prisms etc.

• The different phenomena like dispersion and scattering of light.

• The two aspects of treating light as a ray and a wave.

• The behaviour and propagation of light.

• The concepts related to mirrors, lenses, prisms etc.

• The different optical instruments like microscope, telescope etc.

• The terms like magnification and resolving power etc.

• The various phenomena that support the wave nature of light.

INTRODUCTION

Light is mystical. Yet, its behaviour is so fascinating. It is difficult to comprehend light to a single entity. In this unit, we learn it in two different scientific aspects called ray optics and wave optics. Ray optics deals with light that is represented as a ray travelling in straight lines. Here, the geometrical constructs get the permanence to understand some of the characteristics of light and the phenomena associated with it. There are several other phenomena which can only be explained using wave optics, which we study in the next Unit. There is also a quantum aspect of light which we can study as quantum optics in graduate level courses.

Ray optics

Light travels in a straight line in a medium. Light may deviate in its path only when it encounters another medium or an obstacle.

A ray of light gives information about only the direction of light. It does not give information about the other characteristics of light like intensity and colour. However, a ray is a sensible representation of light in ray optics. The path of the light is called a ray of light and a bundle of such rays is called a beam of light. In this chapter, we can explain the phenomena of reflection, refraction, dispersion and scattering of light, using the ray depiction of light.

Reflection

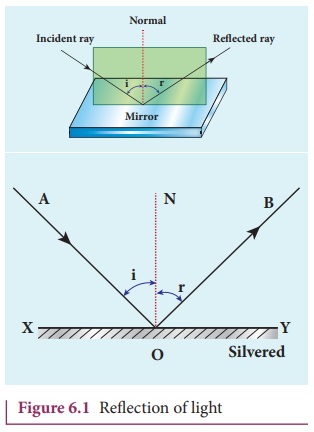
The bouncing back of light into the same medium when it encounters a reflecting surface is called reflection of light. Polished surfaces can reflect light. Mirrors which are silver coated at their back can reflect almost 90% of the light falling on them. The angle of incidence i and the angle of reflection r are measured with respect to the normal drawn to the surface at the point of incidence of light. According to law of reflection,

(a) The incident ray, reflected ray and normal to the reflecting surface all are coplanar (ie. lie in the same plane).

(b) The angle of incidence i is equal to the angle of reflection r.

i = r                       (6.1)

The law of reflection is shown in Figure 6.1.

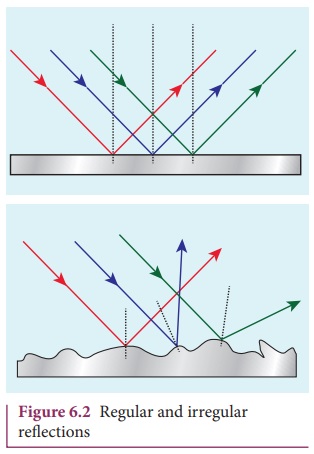
The law of reflection is valid at each point for any reflecting surface whether the surface is plane or curved. If the reflecting surface is flat, then incident parallel rays after reflection come out parallel as per the law of reflection. If the reflecting surface is irregular, then the incident parallel rays after reflection come out irregular (not parallel) rays. Still law of reflection is valid at every point of incidence as shown in Figure 6.2.

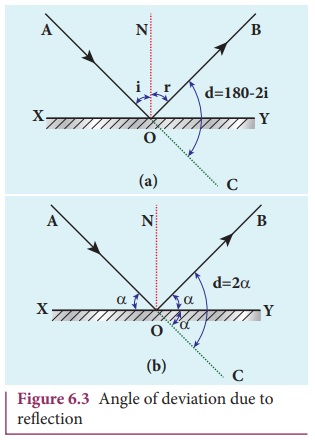
Angle of deviation due to reflection

The angle between the incident and deviated light ray is called angle of deviation of the light ray. In reflection, it is calculated by a simple geometry as shown in Figure 6.3(a). The incident light is AO. The reflected light is OB. The un-deviated light is OC which is the continuation of the incident light. The angle between OB and OC is the angle of deviation d. From the geometry, it is written as, d = 180 – (i+r). As, i = r in reflection, we can write angle of deviation in reflection at plane surface as,

d = 180 – 2i (6.2)

The angle of deviation can also be measured in terms of the glancing angle α which is measured between the incident ray AO and the reflecting plane surface XY as shown in Figure 6.3(b). By geometry, the angles ∠AOX = α, ∠BOY = α and ∠YOC = α (are all same). The angle of deviation (d) is the angle ∠BOC. Therefore,

d = 2α (6.3)

EXAMPLE 6.1

Prove that when a reflecting surface of light is tilted by an angle θ, the reflected light will be tilted by an angle 2θ.

Solution

For the reflecting surface AB, the incident ray IO and the reflected ray OR1 subtend angle i with the normal N as angle of incidence is equal to angle of reflection as shown in figure .

When the surface AB is tilted to A’B’ by an angle θ, the normal N ‘ is also is tilted by the same angle θ. Remember the position of incident ray IO remains unaltered. But, in the tilted system the angle of incidence is now i+θ and the angle of reflection is also i+θ. Now, OR2 is the reflected ray. The angle between OR2 and OR1 is,

∠R1OR2 = ∠N ′OR2 −∠NOR1

(i+θ) – (i–θ) = 2θ.

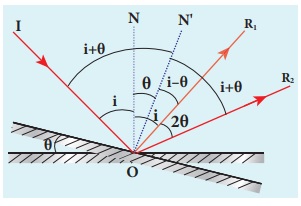
Image formation in plane mirror

Let us consider a point object A is placed in front of a plane mirror and the point of incidence is O on the mirror as shown in the Figure. 6.4. A light ray AO from the point object is incident on the mirror and it is reflected along OB. The normal is ON.

The angle of incidence ∠AON = angle of reflection ∠BON

Another ray AD incident normally on the mirror at D is reflected back along DA. When BO and AD are extended backwards, they meet at a point A’ . Thus, the rays appear to come from a point A’ which is behind the plane mirror. The object and its image in a plane mirror are at equal perpendicular distances from the plane mirror which can be shown by the following explanation.

In Figure 6.4, Angle ∠AON = angle ∠DAO [Since they are alternate angles]

Angle ∠BON = angle ∠OA’D [Since they are corresponding angles]

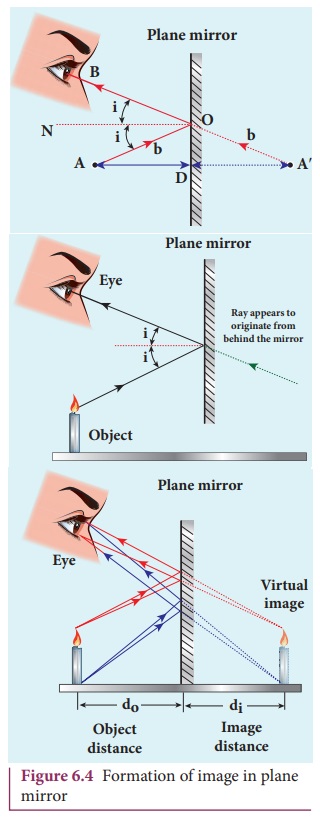
Hence, it follows that angle, ∠DAO = ∠OA’D

The triangles ∆ODA and ∆ODA’ are congruent

∴ AD = A’D

This shows that the image distance inside the plane mirror is equal to the object distance in front of the plane mirror.

Characteristics of the image formed by plane mirror

(i) The image formed by a plane mirror is virtual, erect, and laterally inverted.

(ii) The size of the image is equal to the size of the object.

(iii) The image distance far behind the mirror is equal to the object distance in front of it.

(iv) If an object is placed between two plane mirrors inclined at an angle θ, then the number of images n formed is as,

• If (360/θ) is even then, n = ( 360/θ – 1 ) for objects placed symmetrically or unsymmetrically,

• If (360/θ) is odd then, n = ( 360/θ – 1 ) for objects placed symmetrically,

• If (360/θ) is odd then, n = ( 360/θ) for objects placed unsymmetrically.

Real and virtual images by a plane mirror

When a real object is placed at a point O in front of a plane mirror it produces divergent rays in all directions as shown in Figure 6.5(a). After reflection from the plane mirror they appear to come out from a point I behind the mirror. This image cannot be formed on a screen as the image is behind the mirror. This type of image which cannot be formed on the screen but can only be seen with the eyes is called virtual image.

On the other hand, if convergent rays are incident on a plane mirror, the rays after reflection pass through a point I in front of the mirror and form an image as shown in Figure 6.5(b). This image can be formed on a screen as the image is in front of the mirror. This type of image which canbe formed on a screen and can also be seen with the eyes is called real image.

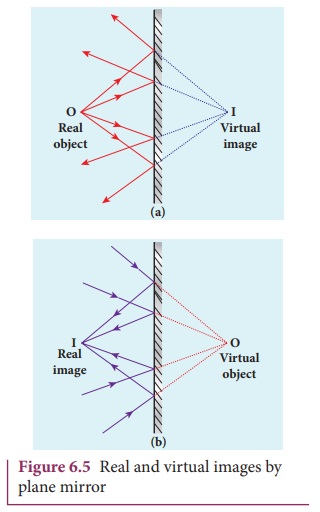
It is generally known that a plane mirror can only form a virtual image. But, now we have understood that a plane mirror can form a real image when converging rays fall on it.

The above discussion is consolidated in Table 6.1. These concepts will be very much useful in deciding about the nature of object and image in ray optics.

Table 6.1 Conditions for nature of objects and images

Nature of object/image: Condition

Real Image: Rays actually converge at the image

Virtual Image: Rays appear to diverge from the image

Real Object: Rays actually diverge from the object

Virtual Object: Rays appear to converge at the object

EXAMPLE 6.2

What is the height of the mirror needed to see the image of a person fully on the mirror?

Solution

Let us assume a person of height h is standing in front of a vertical plane mirror. The person could see his/her head when light from the head falls on the mirror and gets reflected to the eyes. Same way, light from the feet falls on the mirror and gets reflected to the eyes.

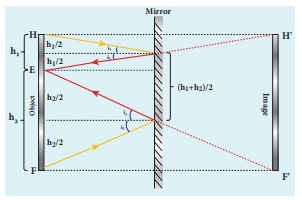
If the distance between his head H and eye E is h1 and distance between his feet F and eye E is h2. The person’s total height h is, h = h1 + h2

By the law of reflection, the angle of incidence and angle of reflection are the same in the two extreme reflections. The normals are now the bisectors of angles between incident and reflected rays in the two reflections. By geometry, the height of the mirror needed is only half of the height of the person. h1 + h2 / 2 = h / 2

Does the height depend on the distance between the person and the mirror?