Prism

PRISM

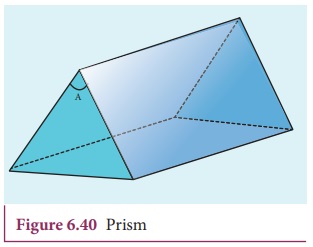
A prism is a triangular block of glass or plastic. It is bounded by the three plane faces not parallel to each other. Its one face is grounded which is called base of the prism. The other two faces are polished which are called refracting faces of the prism. The angle between the two refracting faces is called angle of prism (or) refracting angle (or) apex angle of the prism represented as A as shown in Figure 6.40.

Angle of deviation produced by prism

Let light ray PQ is incident on one of the refracting faces of the prism as shown in Figure 6.41. The angles of incidence and refraction at the first face AB are i₁ and r₁. The path of the light inside the prism is QR. The angle of incidence and refraction at the second face AC is r₂ and i₂ respectively. RS is the ray emerging from the second face. Angle i₂ is also called angle of emergence. The angle between the direction of the incident ray PQ and the emergent ray RS is called the angle of deviation d. The two normals drawn at the point of incidence Q and emergence R are QN and RN. They meet at point N. The incident ray and the emergent ray meet at a point M.

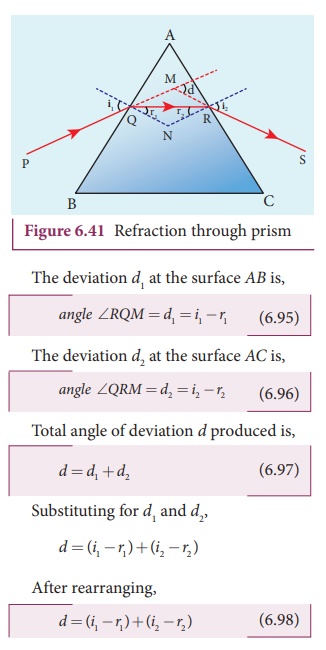
The deviation d₁ at the surface AB is,

In the quadrilateral AQNR, two of the angles (at the vertices Q and R) are right angles. Therefore, the sum of the other angles of the quadrilateral is 180º.

Comparing these two equations (6.99) and (6.100) we get,

Substituting this in equation (6.98) for angle of deviation,

Thus, the angle of deviation depends on the angle of incidence angle of emergence and the angle for the prism. For a given angle of incidence the angle of emergence is decided by the refractive index of the material of the prism. Hence, the angle of deviation depends on these following factors.

(i) the angle of incidence

(ii) the angle of the prism

(iii) the material of the prism

(iv) the wave length of the light

EXAMPLE 6.19

A monochromatic light is incident on an equilateral prism at an angle 30º and emerges at an angle of 75º. What is the angle of deviation produced by the prism?

Solution

Given, as the prism is equilateral,

A = 60°; i₁ = 30°; i₂ = 75°

Equation for angle of deviation, d = i₁ + i₂ – A Substituting the values, d = 30°+75°–60°=45° The angle of deviation produced is, d = 45°

EXAMPLE 6.20

Light ray falls at normal incidence on the first face of anequilateral prism and emerges gracing the second face. What is the angle of deviation? What is the refractive index of the material of the prism?

Solution

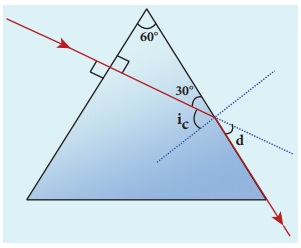
The given situation is shown in the figure.

Here, A = 60°; i₁ = 0°; i₂ = 90°

Equation for angle of deviation,

d = i₁ + i₂ − A

Substituting the values,

d = 0°+ 90°−60° = 30°

The angle of deviation produced is, d = 30°

The light inside the prism must be falling on the second face at critical angle as it graces the boundary.

Equation for critical angle is, sini_c = 1/n

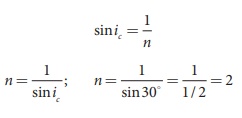
The refractive index of the material of the prism is, n = 2

Angle of minimum deviation

A graph plotted between the angle of incidence and angle of deviation is shown in Figure 6.42. One could observe that the angle of deviation decreases with increase in angle of incidence and reaches a minimum value and then continues to increase.

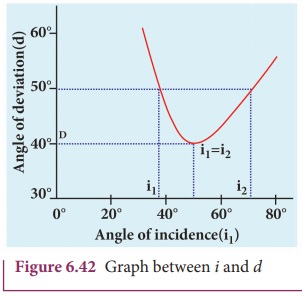
The minimum value of angle of deviation is called angle of minimum deviation D. At minimum deviation,

(a) the angle of incidence is equal to the angle of emergence, i₁=i₂.

(b) the angle of refraction at the face one and face two are equal, r₁=r₂).

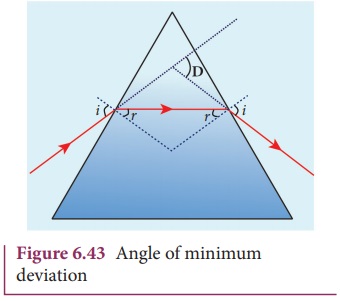
(c) the incident ray and emergent ray are symmetrical with respect to the prism.

(d) the refracted ray inside the prism is parallel to its base of the prism.

The case of angle of minimum deviation is shown in Figure 6.43.

Refractive index of the material of the prism

At minimum deviation, i₁=i₂=i and r₁=r₂=r

Now, the equation (6.102) becomes,

D = i₁ + i₂ - A = 2i − A

(or)

 i = (A + D) / 2

The equation (6.101) becomes,

r₁ + r₂ = = A ⇒ 2r = A

(or)

r = A/2

Substituting i and r in Snell’s law,

The above equation is used to find the refractive index of the material of the prism. The angles A and D can be measured experimentally.

EXAMPLE 6.21

The angle of minimum deviation for a prism is 37º. If the angle of prism is 60º, find the refractive index of the material of the prism.

Solution

Given, A=60°; D=37°

Equation for refractive index is,

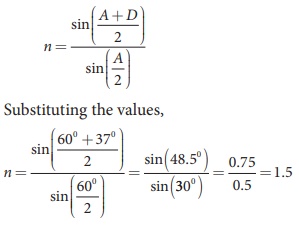
The refractive index of the material of the prism is, n = 1.5

Dispersion of white light through prism

So far the angle of deviation produced by a prism is discussed for monochromatic light (i.e. light of single colour). When white light enter in to a prism, the effect called dispersion takes place. Dispersion is splitting of white light into its constituent colours. This band of colours of light is called its spectrum. When a narrow beam of parallel rays of white light is incident on the face of a prism and the refracted beam is received on a white screen, a band of colours is obtained in the order, recollected by the word: VIBGYOR i.e., Violet, Indigo, Blue, Green, Yellow, Orange and Red. Violet is the most deviated and red is the least deviated colour as shown in Figure 6.44.

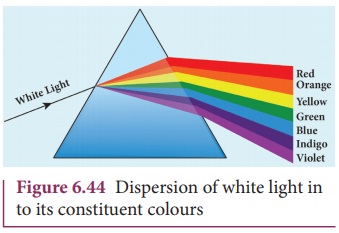
The colours obtained in a spectrum depend on the nature of the source of the light used. Each colour of light is associated with a definite wavelength. Red light is at the longer wavelength end (700 nm) while the violet light is at the shorter wavelength end (400 nm). Therefore the violet ray travels with a smaller velocity in glass prism than red ray.

Points to Ponder

Sir Isaac Newton has demonstrated through a classic experiment to produce white light when all the colours of VIBGYOR are recombined. He used a prism to produce dispersion and made all the colours to incident on another inverted prism to combine all the colours to get white light as shown in figure.

Dispersion takes place because light of different wave lengths travel with different speeds inside the prism. In other words, the refractive index of the material of the prism is different for different colours. For violet, the refractive index is high and for red the refractive index is the low. In Vacuum, all the colours travel with the same speed. The refractive index of two different glasses for different colours is shown in Table 6.4.

The speed of light is independent of wavelength in vacuum. Therefore, vacuum is a non-dispersive medium in which all colours travel with the same speed.

Dispersive Power

Consider a beam of white light passes through a prism; it gets dispersed into its constituent colours as shown in Figure 6.45. Let δ_V, δ_R are the angles of deviation for violet and red light. Let n_V and n_R are the refractive indices for the violet and red light respectively.

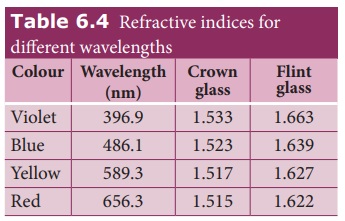
The refractive index of the material of a prism is given by the equation (6.103),

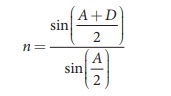
Here A is the angle of the prism and D is the angle of minimum deviation. If the angle of prism is small of the order of 10º, the prism is said to be a small angle prism. When rays of light pass through such prisms, the angle of deviation also becomes small. If A be the angle of a small angle prism and δ the angle of deviation then the prism formula becomes.

When white light enters the prism, the deviation is different for different colours. Thus, the refractive index is also different for different colours.

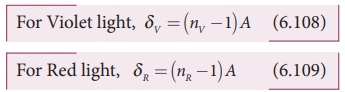
As, angle of deviation for violet colour δ_V is greater than angle of deviation for red colour δ_R, the refractive index for violet colour n_V is greater than the refractive index for red colour n_R.

Subtracting δ_V from δ_R we get,

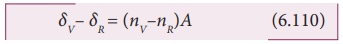
The term (δ_V–δ_R) is the angular separation between the two extreme colours (violet and red) in the spectrum is called the angular dispersion. Clearly, the angular dispersion produced by a prism depends upon.

(i) Angle of the prism

(ii) Nature of the material of the prism.

If we take δ is the angle of deviation for any middle ray (green or yellow) and n the corresponding refractive index. Then,

Dispersive power (ω) is the ability of the material of the prism to cause dispersion. It is defined as the ratio of the angular dispersion for the extreme colours to the deviation for any mean colour.

Dispersive power (ω),

Dispersive power is a dimensionless quality. It has no unit. Dispersive power is always positive. The dispersive power of a prism depends only on the nature of material of the prism and it is independent of the angle of the prism.

EXAMPLE 6.22

Find the dispersive power of flint glass if the refractive indices of flint glass for red, green and violet light are 1.613, 1.620 and 1.632 respectively.

Solution

Given, n_V=1.632; n_R=1.613; n_G=1.620

Equation for dispersive power is,

The dispersive power of flint glass is, ω = 0.0306

Scattering of sunlight

When sunlight enters the atmosphere of the earth, the atmospheric particles present in the atmosphere change the direction of the light. This process is known as scattering of light.

If the scattering of light is by atoms and molecules which have size a very less than that of the wave length λ of light a<<λ, the scattering is called Rayleigh’s scattering. The intensity of Rayleigh’s scattering is inversely proportional to fourth power of wavelength.

According to equation 6.114, violet colour which has the shortest wavelength gets much scattered during day time. The next scattered colour is blue. As our eyes are more sensitive to blue colour than violet colour the sky appears blue during day time as shown in Figure 6.46(a). But, during sunrise and sunset, the light from sun travels a greater distance through the atmosphere. Hence, the blue light which has shorter wavelength is scattered away and the less-scattered red light of longer wavelength manages to reach  our eye. This is the reason for the reddish appearance of sky during sunrise and sunset as shown in Figure 6.46(b).

Rainbow is an example of dispersion of sunlight through droplets of water during rainy days. Rainbow is observed during a rainfall or after the rainfall or when we look at a water fountain provided the sun is at the back of the observer. When sunlight falls on the water drop suspended in air, it splits (or dispersed) into its constituent seven colours. Thus, water drop suspended in air behaves as a glass prism. Primary rainbow is formed when light entering the drop undergoes one total internal reflection inside the drop before coming out from the drop as shown in figure. The angle of view for violet to red in primary rainbow is 40º to 42º. A secondary rainbow appears outside of a primary rainbow and develops when light entering a raindrop undergoes two internal reflections. The angle of view for red to violet in a secondary rainbow is, 52º to 54º.

If light is scattered by large particles like dust and water droplets present in the atmosphere which have size a greater than the wavelength λ of light, a >> λ, the intensity of scattering is equal for all the wavelengths. It is happening in clouds which contains large amount of dust and water droplets. Thus, in clouds all the colours get equally scattered irrespective  of wavelength. This is the reason for the whitish appearance of cloud as shown in Figure 6.46(c). But, the rain clouds appear dark because of the condensation of water droplets on dust particles that makes the cloud become opaque.

If earth has no atmosphere there would not have been any scattering and the sky would appear dark. That is why sky appears dark for the astronauts who could see the sky from above the atmosphere.