with solution and answers | Ray Optics | Physics - All Numerical Problems of Ray Optics | 12th Physics : UNIT 6 : Ray Optics
Chapter: 12th Physics : UNIT 6 : Ray Optics
All Numerical Problems of Ray Optics
Numerical Problems
1. An object of 4 cm height is placed at 6 cm in front of a concave mirror of radius of curvature 24 cm. Find the position, height, magnification and nature of the image.
[Ans: v=12 cm, h'=8 cm, m=2, image is erect, virtual, twice the height of object on right side of mirror.]
Given:
h = 4 cm ; u = -6 cm, R = 24 cm, f = ?
v =? h = ?, m = ?
Solution:
Focal length f = R/2 = 24/2
F = 12 cm
The mirror equvation, 1/f = 1/v + 1/u
1/ -12 = 1/v + 1/-6
1/v = 1/6 – 1/12 = 1/12
∴ v = 12 cm
Magnification (m) = h’/h = - v/u
h’ = h ( -v /u ) = 4 ( -12/-6)
h’ = 8 cm
m = h’ / h = 8/4 = 2
m = 2
∴ Image is erect, virtual, twice the height of object on right side of mirror.
2. An object is placed in front of a concave mirror of focal length 20 cm. The image formed is three times the size of the object. Calculate two possible distances of the object from the mirror.
[Ans: with +m, u = –40/3 cm and with –m, u = –80/3 cm]
Data:
f = -20cm, m = ±3,
Two possible object distance (u) = ?
Solution:
If m = +3
The magnification m = -v/u = 3
∴ v= -3u
The mirror equation is
1/f = 1/v +1/u
-1/20 = 1/-3u + 1/u
-1/20 = 2/3u
3u = -40
u = -40/3 cm
If m = -3
m = -v/u = -3
∴ v = 3u
∴ 1/f = 1/v + 1/u
-1/20 = 1/3u + 1/u
-1/20 = 4/3u
3u = -80
u = -80/3 cm (OR)
Alternate method:
If m = +3 :
m = f / f−u
3= -20 / -20-u = 20 / 20+u
20+u = 20/3
u =20/3 − 20 = 20−60 / 3
∴ u = − 40/3 cm
If m= -3:
m= f / f−u
−3= −20 / -20-u = 20 / 20+u
20 + u = 20 / −3
20+u = 20/-3
u = (20/-3) − 20
∴ u = − 80/3 cm
3. A beam of light consisting of red, green and blue is incident on a right-angled prism as shown in figure. The refractive index of the material of the prism for the above red, green and blue colours are 1.39, 1.44 and 1.47 respectively. What are the colours suffers total internal reflection?
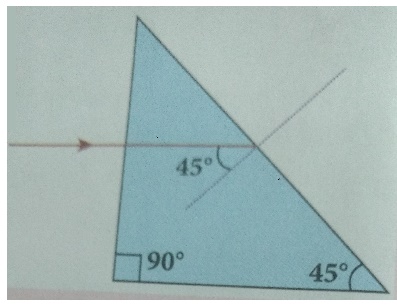
[Ans: green and blue suffer total internal reflection]
Given:
Angle of incidence (i) = 45°
nR = 1.39 ; nG = 1.44, nB = 1.47, ic =?
Solution:
Critical angle (ic) = sin-1 (1/n)
For Red colour:
ic = sin -1(1/ 1.39)
= sin -1 (0.7194)
ic = 460
i < ic ; ∴ It does not suffer total internal reflection.
For Green colour:
ic = sin -1(1/ 1.44)
= sin -1 (0.6944)
ic = 43.90
i < ic ; ∴ It suffer total internal reflection.
For Blue colour:
Ic = sin-1(1/1.47)
= sin-1 (0.6803)
ic = 42.8°
i > ic ; ∴ It suffer total internal reflection.
4. An object is placed at a certain distance from a convex lens of focal length 20 cm. Find the distance of the object if the image obtained is magnified 4 times.
[Ans: –15 cm.]
Data:
f = 20cm, m = 4, u = ?
Solution:
m = v/u = 4
v = 4u
The lens equation is
1/f = 1/v − 1/u
1/f = 1/4u − 1/u
1/f = -3/4u
u = -3f / 4 = − 3 x20 / 4
u = − 15 cm
Alternate method:
m = f / f+u
4 = 20 / (20+u)
20+u = 20/4 = 5
u = −15cm
5. Obtain the lens maker's formula for a lens of refractive index n2 which is separating two media of refractive indices ni and n3 on the left and right respectively.
Solution:

The general equation for the refraction at a spherical surface is
[n2 / v] − [n1 / u] = (n2 − n1) / R
For left side, the light goes from n1 to n2
(n2 / v’ ) – (n1 /u) = (n2 − n1) / R1 --------------------(1)
For right side, the light goes from n2 to n3.
I' acts as virtual object.
n3 / v – n2/v’ = ( n3 − n2 )/ R2 -----------(2)
Adding the equation (1) and (2), we get
[n3 /v] – [n1/u] = [(n2- n1) / R1 ] + [(n3-n2) / R2]
6. A thin converging glass lens made of glass with refractive index 1.5 has a power of + 5.0 D. When this lens is immersed in a liquid of refractive index n, it acts as a divergent lens of focal length 100 cm. What must be the value of n?
[Ans: 5/3]
Given:
n2 = 1.5 ; P = +5.0 D
n (or) n1 = refractive index of liquid = ?
f = 100 cm
Solution:
The lens maker's formula:
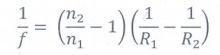
Before immerse in liquid
P=1/f = 5D
n2=1.5
n1=1
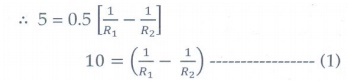
After immersed in liquid
f = −100 cm = −1 m (diverging lens)
1/f = − 1 D
n2=1.5
n1= n
7. If the distance D between an object and screen is greater than 4 times the focal length of a convex lens, then there are two positions of the lens for which images are formed on the screen. This method is called conjugate foci method. If d is the distance between the two positions of the lens, obtain the equation for focal length of the convex lens.
[Ans: ( f = [D2 −d2] / 4D )
The method is called conjugate foci (or) Bessel's method.
Solution:
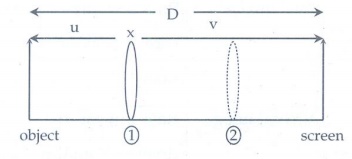
Consider only one position, object distance = - u;
Image distance (v) = D − u
From lens equation
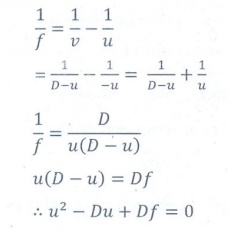
The solution for the quadratic equation is
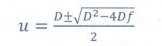
∴ Two possible positions of lens from the object is

Distance between the two position is
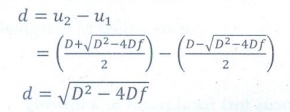
Squaring and rearrange the above equation, we get

8. Prove that a convex mirror can only form a virtual, erect and diminished image.
Solution:
Image formation due to a convex mirror is
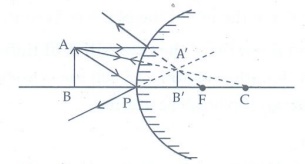
The object placed any where on the principal axis. The convex mirror can only form a virtual, erect and diminished image.
9. A point object is placed at 20 cm from a thin plano-convex lens of focal length 15 cm whose plane surface is silvered. Locate the position and nature of the final image.
[Ans: v = − 12 cm]
Given:
u = -20 cm ; fl =15 cm ; v = ?
Solution:
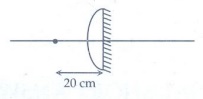
The power P of the silvered lens is
P = 2Pi + Pm

The mirror equation is
1/v + 1/u = 1/f
(1/v) + (1/-20) = −2/15
1/v = (1/20) – (2/15)
∴ v = −12 cm
The negative sign indicates that the image is formed to the left of the plano convex mirror.
10. Find the ratio of the intensities of lights with wavelengths 500 nm and 300 nm which undergo Rayleigh scattering.
[Ans: 81:625]
Given:
λ1 = 500 nm ; λ2 = 300 nm, I1 : I2 = ?
Solution:
According to Rayleigh scattering law
1∝ 1/λ4
∴ The ratio of intensities of light

RAY OPTICS - Numerical Problems Questions with Answers, Solution
EXAMPLE 6.1
Prove that when a reflecting surface of light is tilted by an angle θ, the reflected light will be tilted by an angle 2θ.
Solution
For the reflecting surface AB, the incident ray IO and the reflected ray OR1 subtend angle i with the normal N as angle of incidence is equal to angle of reflection as shown in figure .
When the surface AB is tilted to A’B’ by an angle θ, the normal N ‘ is also is tilted by the same angle θ. Remember the position of incident ray IO remains unaltered. But, in the tilted system the angle of incidence is now i+θ and the angle of reflection is also i+θ. Now, OR2 is the reflected ray. The angle between OR2 and OR1 is,
∠R1OR2 = ∠N ′OR2 −∠NOR1
(i+θ) – (i–θ) = 2θ.

EXAMPLE 6.2
What is the height of the mirror needed to see the image of a person fully on the mirror?
Solution
Let us assume a person of height h is standing in front of a vertical plane mirror. The person could see his/her head when light from the head falls on the mirror and gets reflected to the eyes. Same way, light from the feet falls on the mirror and gets reflected to the eyes.
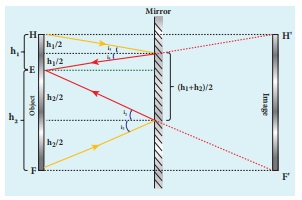
If the distance between his head H and eye E is h1 and distance between his feet F and eye E is h2. The person’s total height h is, h = h1 + h2
By the law of reflection, the angle of incidence and angle of reflection are the same in the two extreme reflections. The normals are now the bisectors of angles between incident and reflected rays in the two reflections. By geometry, the height of the mirror needed is only half of the height of the person. h1 + h2 / 2 = h / 2
SPHERICAL MIRRORS - Numerical Problems Questions with Answers, Solution
EXAMPLE 6.3
An object is placed at a distance of 20.0 cm from a concave mirror of focal length 15.0 cm.
(a) What distance from the mirror a screen should be placed to get a sharp image?
(b) What is the nature of the image?
Solution
Given, f = –15 cm, u = –20 cm

As the image is formed at 60.0 cm to the left of the concave mirror, the screen is to be placed at distance 60.0 cm to the left of the concave mirror.
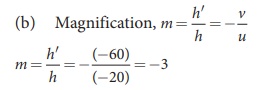
As the sign of magnification is negative, the image is inverted.
As the magnitude of magnification is 3, the image is enlarged three times.
As the image is formed to the left of the concave mirror, the image is real.
EXAMPLE 6.4
A thin rod of length f /3 is placed along the optical axis of a concave mirror of focal length f such that its image which is real and elongated just touches the rod. Calculate the longitudinal magnification.
Solution
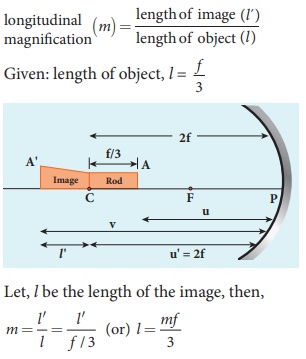
Image of one end coincides with the object.
Thus, the coinciding end must be at center of curvature.
Hence, u’ = R = 2f

Speed of Light - Numerical Problems Questions with Answers, Solution
EXAMPLE 6.5
One type of transparent glass has refractive index 1.5. What is the speed of light through this glass?
Solution
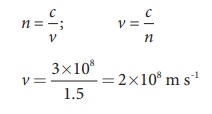
Light travels with a speed of 2 × 108 ms-1 through this glass.
EXAMPLE 6.6
Light travels from air in to glass slab of thickness 50 cm and refractive index 1.5.
(i) What is the speed of light in glass?
(ii) What is the time taken by the light to travel through the glass slab?
(iii) What is the optical path of the glass slab?
Solution
Given, thickness of glass slab, d = 50 cm = 0.5 m, refractive index, n = 1.5
refractive index, n = c/v
speed of light in glass is,
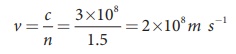
Time taken by light to travel through glass slab is,
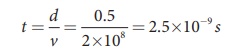
Optical path,
d′ = nd = 1.5×0.5 = 0.75 m = 75 cm
Light would have travelled 25 cm more (75 cm – 50 cm) in vacuum by the same time had there not been a glass slab.
Refraction - Numerical Problems Questions with Answers, Solution
EXAMPLE 6.7
Light travelling through transparent oil enters in to glass of refractive index 1.5. If the refractive index of glass with respect to the oil is 1.25, what is the refractive index of the oil?
Solution
Given, ngo =1.25 and ng =1.5
Refractive index of glass with respect to oil,
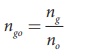
Rewriting for refractive index of oil,
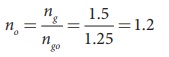
The refractive index of oil is, no = 1.2
EXAMPLE 6.8
A coin is at the bottom of a trough containing three immiscible liquids of refractive indices 1.3, 1.4 and 1.5 poured one above the other of heights 30 cm, 16 cm, and 20 cm respectively. What is the apparent depth at which the coin appears to be when seen from air medium outside? In which medium the coin will be seen?
Solution
When seen from top, the coin will still appear to be at the bottom with each medium appearing to have shrunk with respect to the air medium outside. This situation is illustrated below.
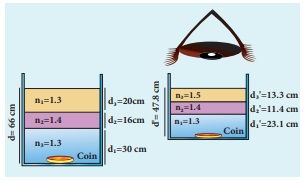
The equations for apparent depth for each medium is,

Effects due to total internal reflection - Numerical Problems Questions with Answers, Solution
EXAMPLE 6.9
What is the radius of the illumination when seen above from inside a swimming pool from a depth of 10 m on a sunny day? What is the total angle of view? [Given, refractive index of water is 4/3]
Solution
Given, n = 4/3, d = 10 m.

The total angle of view is,
2ic = 2 × 48.6º = 97.2º
EXAMPLE 6.10
A optical fibre is made up of a core material with refractive index 1.68 and a cladding material of refractive index 1.44. What is the acceptance angle of the fibre kept in air medium? What is the answer if there is no cladding?
Solution
Given, n1 = 1.68, n2 = 1.44, n1 = 1
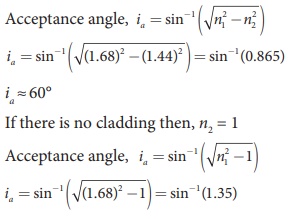
sin−1 (more than 1) is not possible. But, this includes the range 0º to 90º. Hence, all the rays entering the core from flat surface will undergo total internal reflection.
Note: If there is no cladding then there is a condition on the refractive index (n1) of the core.
ia = sin−1(√[n12 −1])
Here, as per mathematical rule, (n2 −1) ≤ 1 or (n12 )≤ 2
or n1 ≤ √2
Hence, in air (no cladding) the refractive index n1 of the core should be, n1 ≤ 1.414
Refraction in glass slab - Numerical Problems Questions with Answers, Solution
EXAMPLE 6.11
The thickness of a glass slab is 0.25 m. it has a refractive index of 1.5. A ray of light is incident on the surface of the slab at an angle of 60º. Find the lateral displacement of the light when it emerges from the other side of the mirror.
Solution
Given, thickness of the slab, t = 0.25 m, refractive index, n = 1.5, angle of incidence, i = 60º.
Using Snell’s law, 1 × sin i = n sin r
sinr = sini / n = sin60 / 1.5 = 0.58
r = sin−1 0.58 = 35.25º

The lateral displacement is, L = 12.81 cm
Refraction at Single Spherical Surface - Numerical Problems Questions with Answers, Solution
EXAMPLE 6.12
Locate the image of the point object O in the situation shown. The point C denotes the centre of curvature of the separating surface.
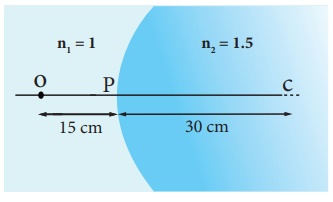
Solution
Given, u = –15 cm, R = 30 cm, n1 = 1 and n2 = 1.5
Equation for single spherical surface is,

v = –30 cm
The image is a virtual image formed 30 cm to the left of the spherical surface.
EXAMPLE 6.13
Find the size of the image formed in the given figure.

Solution
Given, u = –40 cm, R = –20 cm, n1 = 1 and n2 = 1.33
Equation for single spherical surface is,

= 0.6cm (or) h = 0.6cm
The erect virtual image of height 0.6 cm is formed at 32.0 cm to the left of the single spherical surface.
Thin Lens - Numerical Problems Questions with Answers, Solution
EXAMPLE 6.14
A biconvex lens has radii of curvature 20 cm and 15 cm each. The refractive index of the material of the lens is 1.5. What is its focal length? Will the focal length change if the lens is flipped by the side?
Solution
For a biconvex lens, radius of curvature of the first surface is positive and that of the second surface is negative side as shown in the figure.
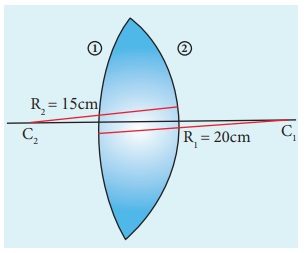
Given, n = 1.5, R1=20 cm and R2= –15 cm
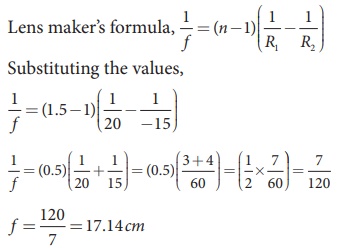
As the focal length is positive the lens is a converging lens.
If the lens is flipped back to front,
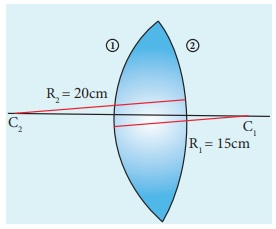
Now, R1= 15 cm and R2= –20 cm, n = 1.5 Substituting the values,
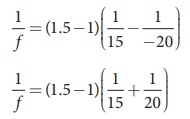
This will also result in, f = 17.14 cm
Thus, it is concluded that the focal length of the lens will not change if it is flipped side wise. This is true for any lens. Students can verify this for any lens.
EXAMPLE 6.15
Determine the focal length of the lens made up of a material of refractive index 1.52 as shown in the diagram. (Points C1 and C2 are the centers of curvature of the first and second surface.)
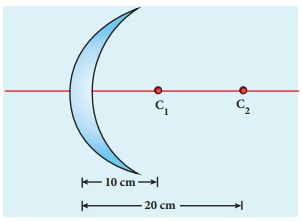
Solution
This lens is called convexo-concave lens
Given, n = 1.52, R1= 10 cm and R2= 20 cm
Lens makers formula,
1/ f = (n −1)( 1/R1 – 1/R2 ) Substituting the values,

As the focal length is positive, the lens is a converging lens.
EXAMPLE 6.16
If the focal length is 150 cm for a glass lens, what is the power of the lens?
Solution
Given, focal length, f = 150 cm (or) f = 1.5 m
Equation for power of lens is, P = 1/f
Substituting the values,
P = 1/1.5 = 0.67diopter
As the power is positive, it is a converging lens.
EXAMPLE 6.17
What is the focal length of the combination if a lens of focal length –70 cm is brought in contact with a lens of focal length 150 cm? What is the power of the combination?
Solution
Given, focal length of first lens, f1 = –70 cm, focal length of second lens, f2 = 150 cm.
Equation for focal length of lenses in contact, 1/F = 1/f1 + 1/f2
Substituting the values,

As the focal length is negative, the combination of two lenses is a diverging system of lenses.
The power of combination is,
P = 1/F = 1/-1.3125m = 0.76 diopter
EXAMPLE 6.18
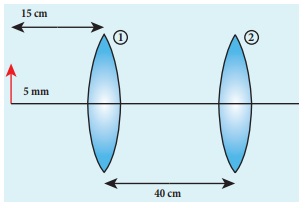
An object of 5 mm height is placed at a distance of 15 cm from a convex lens of focal length 10 cm. A second lens of focal length 5 cm is placed 40 cm from the first lens and 55 cm from the object. Find (a) the position of the final image, (b) its nature and (c) its size.
Solution
Given, h1= 5 mm = 0.5 cm, u1 = –15 cm,
f1 = 10 cm, f2 = 5 cm, d = 40 cm
For the first lens, the lens equation is,

First lens forms image 30 cm to the right of first lens.
Let us find the height of this image.
Equation for magnification is, m = h2/ h1 = v/u
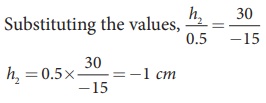
As the height of the lens is negative, the image is inverted, real image.
Object is at 10 cm to the left of the second lens (40–30=10 cm). Hence, u2 = –10 cm
For the second, the lens equation is,

The image is formed 10 cm to the right of the second lens.
Let us find the height of the final image. Assume, the final height of the image formed by the second lens is h2’ and the height of the object for the second lens h1’ is the image height of the first lens, h1′ = h2′

As the height of the image is positive, the image is erect, and it is real.
EXAMPLE 6.18
A thin bicnvex lens is made up of a glass of refractive index 1.5. The two surfaces have equal radii of curvature of 30 cm each. One of its surfaces is made reflecting by silvering it from outside. (a) What is the focal length and power of this silvered lens? (b) Where should an object be placed in front of this lens so that the image is formed on the object itself?
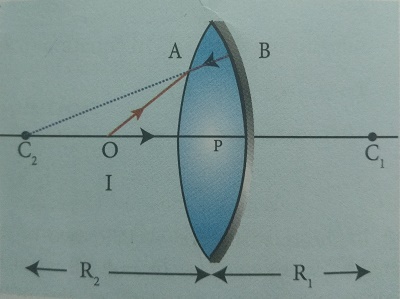
Solution
Given, n = 1.5; R₁ = 30 cm; R2 = -30 cm;
(a) Let us find f1 and f2 separately.
Using lens maker's formula we can find f1.

f1= 30 cm = 0.3 m
Focal length of mirror is, fm = R2 /2
Substituting the values, fm = −30 /2 = − 15cm
fm = 15 cm = − 0.15 m
Now the focal length of the slivered lens is,
1 /−f = 2/f1 + 1/−fm
= 2/30 + 1/15 = 2/15 = 1/7.5
f = −7.5 cm = −0.075 m
The silvered mirror behaves as a concave mirror with its focal length on left side.
Prism - Numerical Problems Questions with Answers, Solution
EXAMPLE 6.19
A monochromatic light is incident on an equilateral prism at an angle 30º and emerges at an angle of 75º. What is the angle of deviation produced by the prism?
Solution
Given, as the prism is equilateral,
A = 60°; i1 = 30°; i2 = 75°
Equation for angle of deviation, d = i1 + i2 – A Substituting the values, d = 30°+75°–60°=45° The angle of deviation produced is, d = 45°
EXAMPLE 6.20
Light ray falls at normal incidence on the first face of anequilateral prism and emerges gracing the second face. What is the angle of deviation? What is the refractive index of the material of the prism?
Solution
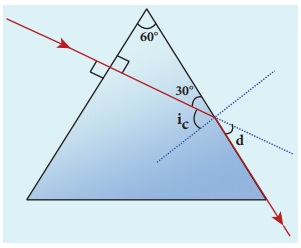
The given situation is shown in the figure.
Here, A = 60°; i1 = 0°; i2 = 90°
Equation for angle of deviation,
d = i1 + i2 − A
Substituting the values,
d = 0°+ 90°−60° = 30°
The angle of deviation produced is, d = 30°
The light inside the prism must be falling on the second face at critical angle as it graces the boundary.
Equation for critical angle is, sinic = 1/n
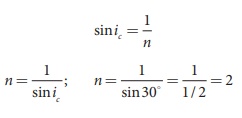
The refractive index of the material of the prism is, n = 2
EXAMPLE 6.21
The angle of minimum deviation for a prism is 37º. If the angle of prism is 60º, find the refractive index of the material of the prism.
Solution
Given, A=60°; D=37°
Equation for refractive index is,
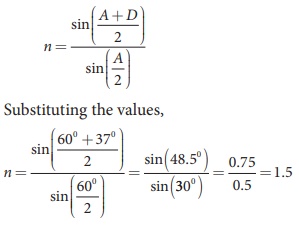
The refractive index of the material of the prism is, n = 1.5
EXAMPLE 6.22
Find the dispersive power of flint glass if the refractive indices of flint glass for red, green and violet light are 1.613, 1.620 and 1.632 respectively.
Solution
Given, nV=1.632; nR=1.613; nG=1.620
Equation for dispersive power is,

The dispersive power of flint glass is, ω = 0.0306
Related Topics