Optics | Physics - Effects due to total internal reflection | 12th Physics : UNIT 6 : Ray Optics
Chapter: 12th Physics : UNIT 6 : Ray Optics
Effects due to total internal reflection
Effects due to total internal reflection
1. Glittering of diamond
Diamond appears dazzling because the
total internal reflection of light happens inside the diamond. The refractive
index of only diamond is about 2.417. It is much larger than that for ordinary
glass which is about only 1.5. The critical angle of diamond is about 24.4°. It
is much less than that of glass. A skilled diamond cutter makes use of this
larger range of angle of incidence (24.4° to 90° inside the diamond), to ensure
that light entering the diamond is total internally reflected from the many cut
faces before getting out as shown in Figure 6.22. This gives a sparkling effect
for diamond.

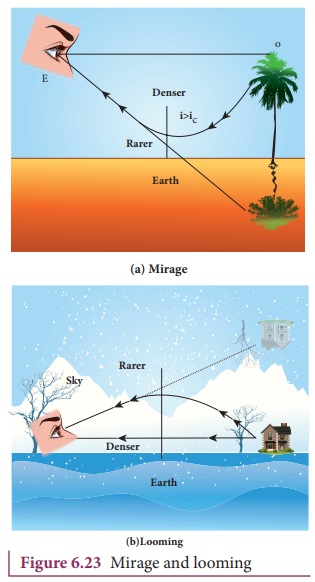
2. Mirage and looming
The refractive index of air
increases with its density. In hot places, air near the ground is hotter than
air at a height. Hot air is less dense. Hence, in still air the refractive
index of air increases with height. Because of this, light from tall objects
like a tree, passes through a medium whose refractive index decreases towards
the ground. Hence, a ray of light successively deviates away from the normal at
different layers of air and undergoes total internal reflection when the angle
of incidence near the ground exceeds the critical angle. This gives an illusion
as if the light comes from somewhere below the ground. For of the shaky nature
of the layers of air, the observer feels as if the object is getting reflected
by a pool of water or wet surface beneath the object as shown in Figure
6.23(a). This phenomenon is called mirage.
In the cold places the refractive
index increases towards the ground because the temperature of air close to the
ground is lesser than the temperature above the surface of earth. Thus, the
density and refractive index of air near the ground is greater than at a
height. In the cold regions like glaciers and frozen lakes and seas, the
reverse effect of mirage will happen. Hence, an inverted image is formed little
above the surface as shown in Figure 6.23(b). This phenomenon is called looming.
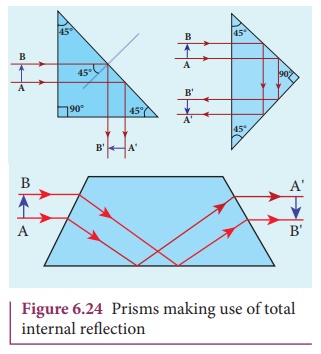
3. Prisms making using of total internal reflection
Prisms can be designed to reflect
light by 90º or by 180º by making use of total internal reflection as shown in
Figure 6.24(a) and (b). In the first two cases, the critical angle ic for the material of the
prism must be less than 45º. We see from Table 6.3 that this is true for both
crown glass and flint glass. Prisms are also used to invert images without
changing their size as shown in Figure. 6.24(c).
4. Radius of illumination (Snell’s window)
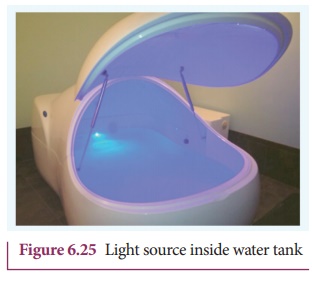
When a light source like electric
bulb is kept inside a water tank, the light from the source travels in all
direction inside the water. The light that is incident on the water surface at
an angle less than the critical angle will undergo refraction and emerge out
from the water. The light incident at an angle greater than critical angle will
undergo total internal reflection.The light falling particularly at critical
angle graces the surface.Thus, the entire surface of water appears illuminated
when seen from outside as shown in Figure 6.25.
On the other hand, when light
entering the water from outside is seen from inside the water, the view is
restricted to a particular angle equal to the critical angle ic. The restricted illuminated circular area is called Snell’s window as shown in Figure 6.26(a).The
Figure 6.26(b) shows the angle of view for water animals.

The angle of view for water animals
is restricted to twice the critical angle 2ic.
The critical angle for water is 48.6º. Thus the angle of view is 97.2 º. The
radius R of the circular area depends
on the depth d from which it is seen
and also the refractive indices of the media.
The radius of Snell’s window can be deduced with the illustration as shown in Figure
6.27.
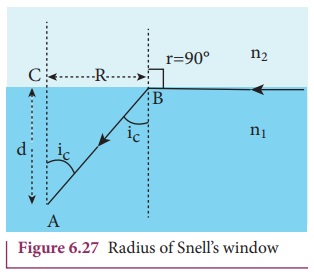
Light is seen from a point A at a depth d. The Snell’s law in product form, equation (6.19) for the
refraction happening at the point B on
the boundary between the two media is,

Equating the above two equation 6.34 and equation 6.35,

If the rarer medium outside is air,
then, n2 = 1, and we can
take n1=n
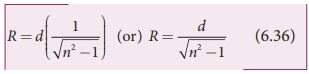
EXAMPLE 6.9
What is the radius of the
illumination when seen above from inside a swimming pool from a depth of 10 m
on a sunny day? What is the total angle of view? [Given, refractive index of
water is 4/3]
Solution
Given, n = 4/3, d = 10 m.

The total angle of view is,
2ic = 2 × 48.6º = 97.2º
5. Optical fiber
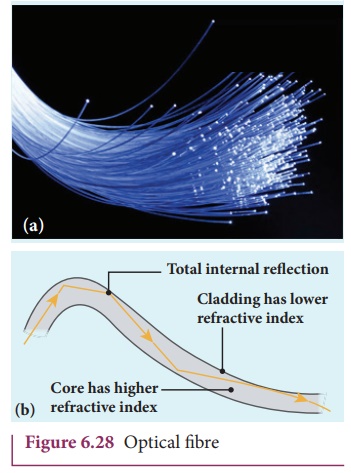
Transmitting signals through optical
fibres is possible due to the phenomenon of total internal reflection. Optical fibres consists of inner part
called core and outer part called cladding (or) sleeving. The refractive index of the material of the core must
be higher than that of the cladding for total internal reflection to happen.
Signal in the form of light is made to incident inside the core-cladding
boundary at an angle greater than the critical angle. Hence, it undergoes
repeated total internal reflections along the length of the fibre without
undergoing any refraction. The light travels inside the core with no
appreciable loss in the intensity of the light as shown in Figure 6.28(a). Even
while bending the optic fiber, it is done in such a way that the condition for
total internal reflection is ensured at every reflection as shown in Figure
6.28(b).
6. Acceptance angle in optical fibre
To ensure the critical angle
incidence in the core-cladding boundary inside the optical fibre, the light
should be incident at a certain angle at the end of the optical fiber while
entering in to it. This angle is called acceptance angle. It depends on the
refractive indices of the core n1,
cladding n2 and the outer
medium n3. Assume the
light is incident at an angle called acceptance angle ia at the outer medium and core boundary at A.
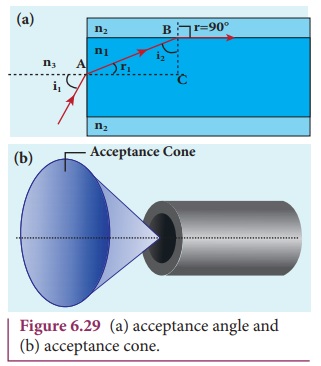
The Snell’s law in the product form,
equation (6.19) for this refraction at the point A is as shown in the Figure 6.29(a),

To have the total internal
reflection inside optical fibre, the angle of incidence at the core-cladding
interface at B should be atleast
critical angle ic. Snell’s
law in the product form, equation (6.19) for the refraction at point B is,

If outer medium is air, then n3 = 1. The acceptance angle ia becomes,
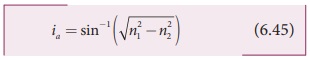
Light can have any angle of incidence
from 0 to ia with the
normal at the end of the optical fibre forming a conical shape called acceptance
cone as shown in Figure 6.29(b). In the equation (6.42), the term (n3 sin ia)
is called numerical aperture NA of the optical fibre.
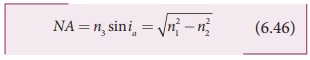
If outer medium is air, then n3= 1. The numerical aperture NA becomes,
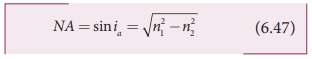
EXAMPLE 6.10
A optical fibre is made up of a core
material with refractive index 1.68 and a cladding material of refractive index
1.44. What is the acceptance angle of the fibre kept in air medium? What is the
answer if there is no cladding?
Solution
Given, n1 = 1.68, n2 = 1.44,
n1 = 1
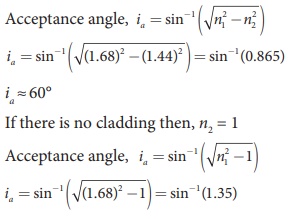
sin−1 (more than 1) is not possible.
But, this includes the range 0º to 90º. Hence, all
the rays entering the core from flat surface will undergo total internal
reflection.
Note: If there is no cladding then there
is a condition on the refractive index (n1)
of the core.
ia = sin−1(√[n12
−1])
Here, as per
mathematical rule, (n2 −1)
≤ 1 or (n12 )≤ 2
or n1 ≤ √2
Hence, in
air (no cladding) the refractive index n1
of the core should be, n1 ≤
1.414
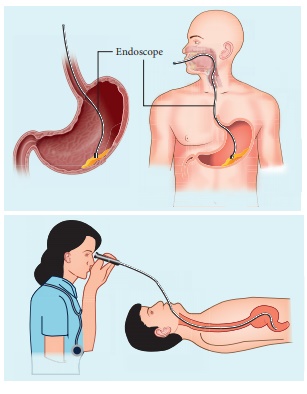
An endoscope is an instrument used
by doctors which has a bundle of optical fibres that are used to see inside a
patient’s body. Endoscopes work on the phenomenon of total internal reflection.
The optical fibres are inserted in to the body through mouth, nose or a special
hole made in the body. Even operations could be carried out with the endoscope
cable which has the necessary instruments attached at their ends.
Related Topics