Refraction

REFRACTION

Refraction is passing through of light from one optical medium to another optical medium through a boundary. In refraction, the angle of incidence i in one medium and the angle of reflection r in the other medium are measured with respect to the normal drawn to the surface at the point of incidence of light. Law of refraction is called Snell’s law.

Snell’s law states that,

a) The incident ray, refracted ray and normal to the refracting surface are all coplanar (ie. lie in the same plane).

b) The ratio of angle of incident i in the first medium to the angle of reflection r in the second medium is equal to the ratio of refractive index of the second medium n₂ to that of the refractive index of the first medium n₁.

The above equation is in the ratio form. It can also be written in a much useful product form as,

The refraction at a boundary is shown in Figure 6.15.

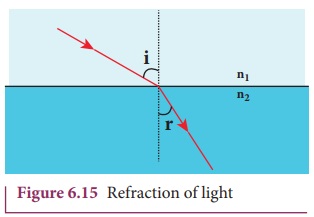
For normal incidence of light on a surface, the angle of incidence is zero.

Angle of deviation due to refraction

We know that the angle between the incident and deviated light is called angle of deviation. When light travels from rarer to denser medium it deviates towards normal as shown in Figure 6.16. The angle of deviation in this case is,

On the other hand, if light travels from denser to rarer medium it deviates away from normal as shown in Figure 6.17. The angle of deviation in this case is,

Characteristics of refraction

a) When light passes from rarer medium to denser medium it deviates towards normal in the denser medium.

b) When light passes from denser medium to rarer medium it deviates away from normal in the rarer medium.

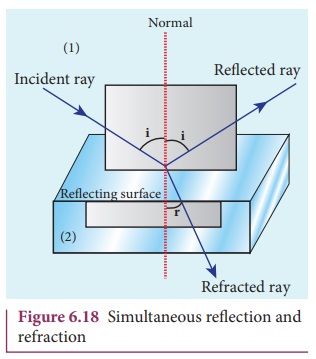
c) In any refracting surface there will also be some reflection taking place. Thus, the intensity of refracted light will be lesser than the incident light. The phenomenon in which a part of light from a source undergoing reflection and the other part of light from the same source undergoing refraction at the same surface is called simultaneous reflection or simultaneous refraction. This is shown in Figure 6.18. Such surfaces are available as partially silvered glasses.

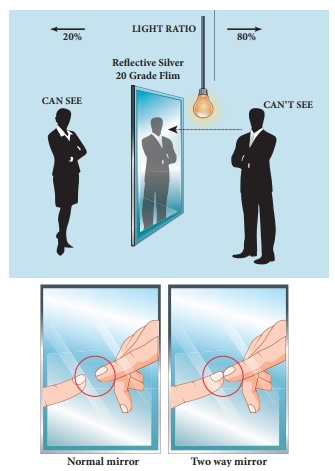
Production of optical surfaces capable of refracting as well as reflecting is possible by properly coating the surfaces with suitable materials. Thus, a glass can be made partially see through and partially reflecting by varying the amount of coating on its surface. It is commercially called as two way mirror, half-silverd or semi-silvered mirror etc. This gives a perception of regular mirror if the other side is made dark. But, still hidden cameras can be kept behind such mirrors. We need to be cautious when we stand in front of mirrors kept in unknown places.

There is a method to test the two way mirror. Place the finger nail against the mirror surface. If there is a gap between nail and its image, then it is a regular mirror. If the fingernail directly touches its image, then it is a two way mirror.

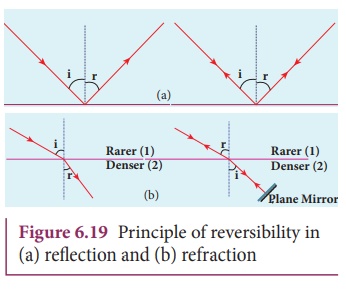
Principle of reversibility

The principle of reversibility states that light will follow exactly the same path if its direction of travel is reversed. This is true for both reflection and refraction as shown in Figure 6.19.

Relative refractive index

In the equation for Snell’s law, the term (n₂/n₁) is callled relative refractive index of second medium with respect to the first medium which is denoted as (n₂₁).

The concept of relative refractive index gives rise to other useful relation such as,

a) Inverse rule:

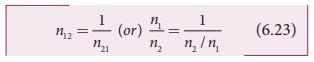
b) Chain rule:

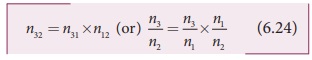
EXAMPLE 6.7

Light travelling through transparent oil enters in to glass of refractive index 1.5. If the refractive index of glass with respect to the oil is 1.25, what is the refractive index of the oil?

Solution

Given, n_go =1.25 and n_g =1.5

Refractive index of glass with respect to oil,

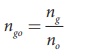
Rewriting for refractive index of oil,

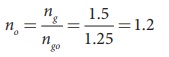
The refractive index of oil is, n_o = 1.2

Apparent depth

It is a common observation thatthebottom of a tank filled with water appears raised as shown in Figure 6.19(a). An equation could be derived for the apparent depth for viewing in the near normal direction. The ray diagram is shown in Figure 6.19(b) and (c).

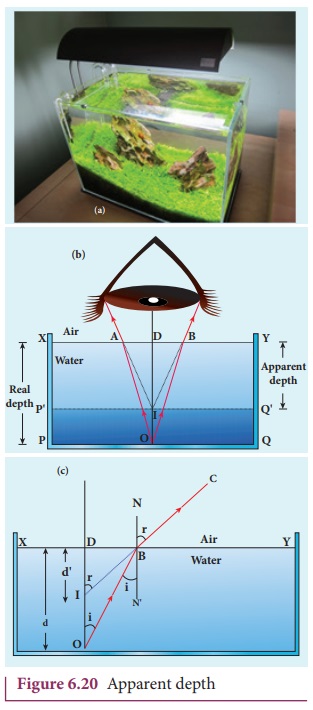
Light from the object O at the bottom of the tank passes from denser medium (water) to rarer medium (air) to reach our eyes. It deviates away from the normal in the rarer medium at the point of incidence B. The refractive index of the denser medium is n₁ and rarer medium is n₂. Here, n₁ > n₂. The angle of incidence in the denser medium is i and the angle of refraction in the rarer medium is r. The lines NN ‘ and OD are parallel. Thus angle ∠DIB is also r. The angles i and r are very small as the diverging light from O entering the eye is very narrow. The Snell’s law in product form for this refraction is,

As the angles i and r are small, we can approximate, sin i ≈ tan i;

n₁ tani = n₂ tan i

In triangles ∆DOB and ∆DIB,

tan(i) = DB/ DO

and tan(r) = DB/DI

n₁ DB/DO = n₂ DB/DI

DB is cancelled on both sides, DO is the actual depth d and DI is the apparent depth d'.

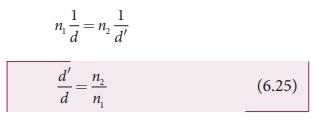
Rearranging the above equation for the apparent depth d',

As the rarer medium is air and its refractive index n₂ can be taken as 1, (n₂=1). And the refractive index n₁ of denser medium could then be taken as n, (n₁=n).

In that case, the equation for apparent depth becomes,

The bottom appears to be elevated by d-d’.

EXAMPLE 6.8

A coin is at the bottom of a trough containing three immiscible liquids of refractive indices 1.3, 1.4 and 1.5 poured one above the other of heights 30 cm, 16 cm, and 20 cm respectively. What is the apparent depth at which the coin appears to be when seen from air medium outside? In which medium the coin will be seen?

Solution

When seen from top, the coin will still appear to be at the bottom with each medium appearing to have shrunk with respect to the air medium outside. This situation is illustrated below.

The equations for apparent depth for each medium is,

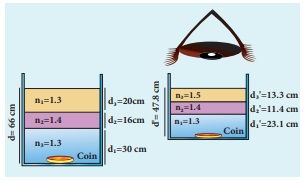
Atmospheric refraction: Due to refraction of light through different layers of atmosphere which vary in refractive index, the path of light deviates continuously when it passes through atmosphere. For example, the Sun is visible a little before the actual sunrise and also until a little after the actual sunset due to refraction of light through the atmosphere. By actual sunrise what we mean is the actual crossing of the sun at the horizon. Figure shows the actual and apparent positions of the sun with respect to the horizon. The figure is highly exaggerated to show the effect. The apparent shift in the direction of the sun is around half a degree and the corresponding time difference between actual and apparent positions is about 2 minutes. Sun appears flattened (oval shaped) during sun rise and sunset due to the same phenomenon.

The same is also applicable for the positions of stars as shown in Figure. The stars actually do not twinkle. They appear twinkling because of the movement of the atmospheric layers with varying refractive indices which is clearly seen in the night sky.

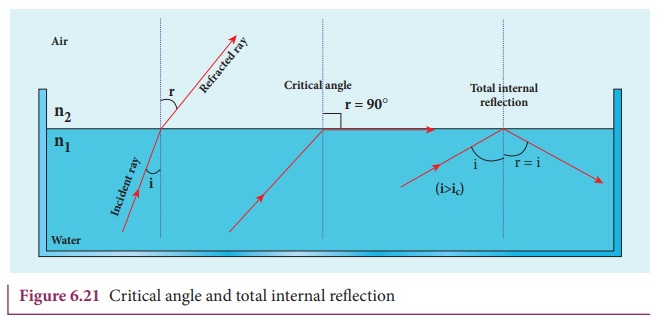
Critical angle and total internal reflection

When a ray passes from an optically denser medium to an optically rarer medium, it bends away from normal. Because of this, the angle of refraction r on the rarer medium is greater than the corresponding angle of incidence i in the denser medium. As angle of incidence i is gradually increased, r rapidly increases and at a certain stage it becomes 90° or gracing the boundary. The angle of incidence in the denser medium for which the refracted ray graces the boundary is called critical angle i_c.

If the angle of incidence in the denser medium is increased beyond the critical angle, there is no refraction possible in to the rarer medium. The entire light is reflected back into the denser medium itself. This phenomenon is called total internal reflection. These are shown in Figure 6.21.

The two conditions for total internal reflection are,

(a) light must travel from denser to rarer medium,

(b) angle of incidence in the denser medium must be greater than critical angle (i>i_c).

Snell’s law in the product form, equation (6.19) for critical angle incidence becomes,

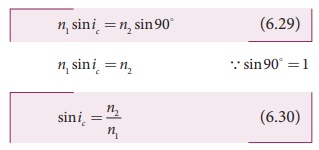
Here, n₁ > n₂

If the rarer medium is air, then its refractive index is 1 and can be taken as n itself. i.e. (n₂=1) and (n₁=n).

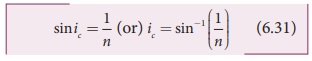
For example the refractive index of glass is about 1.5. The critical angle for glass-air interface is, i_c = sin⁻¹(1/1.5) = 41.8º.

The critical angle for water-air interface is, i_c = sin⁻¹(1/1.3) = 48.6 º.

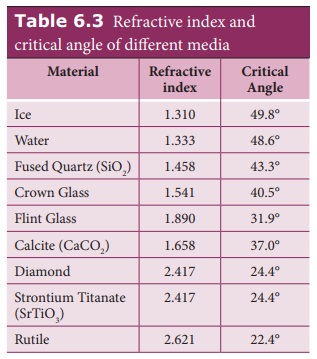
The critical angle ic depends on the refractive index of the medium. Table 6.3 shows the refractive index and the critical angle for different materials.