Refraction at Single Spherical Surface

REFRACTION AT SINGLE SPHERICAL SURFACE

We have so far studied only the refraction at a plane surfaces. The refractions also do take place at spherical surface between two transparent media. The laws of refraction hold good at every point on the spherical surface. The normal at the point of incidence is perpendicular to the tangent plane to the spherical surface at that point. Therefore, the normal always passes through its center of curvature. The study of refraction at single spherical surface paves way to the understanding of thin lenses which consist of two surfaces of which one or both must be spherical.

The following assumptions are made while considering refraction at spherical surfaces.

(a) The incident light is assumed to be monochromatic (single colour)

(b) The incident ray of light is very close to the principal axis (paraxial rays).

The sign conventions are similar to that of the spherical mirrors.

Equation for refraction at single spherical surface

Let us consider two transparent media having refractive indices n₁ and n₂ are separated by a spherical surface as shown in Figure 6.31. Let C be the centre of curvature of the spherical surface. Let a point object O be in the medium n₁. The line OC cuts the spherical surface at the pole P of the surface. As the rays considered are paraxial rays, the perpendicular dropped for the point of incidence to the principal axis is very close to the pole or passes through the pole itself.

Light from O falls on the refracting surface at N. The normal drawn at the point of incidence passes through the centre of curvature C. As n₂>n₁, light in the denser medium deviates towards the normal and meets the principal axis at I where the image is formed.

Snell’s law in product form for the refraction at the point N could be written as,

As the angles are small, sine of the angle could be approximated to the angle itself.

Let the angles,

∠NOP = α, ∠NCP = β, ∠NIP = γ

tanα = PN/PO ; tanβ = PN/PC ; tanγ = PN/PI

As these angles are small, tan of the angle could be approximated to the angle itself.

Substituting for i and r from equations (6.53) and (6.54) in the equation (6.51).

n₁(α + β) = n₂ (β − γ)

Rearranging,

n₁α + n₂γ = (n₂ −n₁)β

Substituting for α, β and γ from equation (6.52),

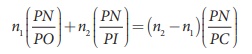
Further simplifying by cancelling PN,

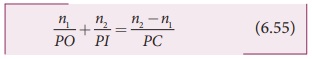
Following sign conventions, PO = –u, PI = +v and PC = +R in equation (6.58),

Equation (6.56) gives the relation among the object distance u, image distance v, refractive indices of the two media (n₁ and n₂ ) and the radius of curvature R of the spherical surface. It holds for any spherical surface.

If the first medium is air then, n₁ = 1 and the second medium is taken just as n₂ = n, then the equation is reduced to,

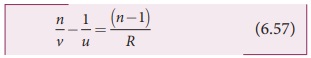
EXAMPLE 6.12

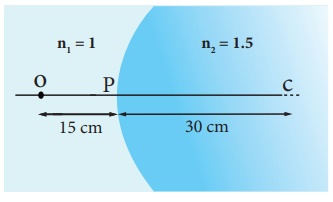
Locate the image of the point object O in the situation shown. The point C denotes the centre of curvature of the separating surface.

Solution

Given, u = –15 cm, R = 30 cm, n₁ = 1 and n₂ = 1.5

Equation for single spherical surface is,

v = –30 cm

The image is a virtual image formed 30 cm to the left of the spherical surface.

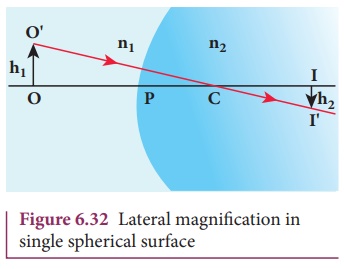
Lateral magnification in single spherical surface

Let us, consider an extended object OO’ is kept perpendicular to the principal axis to the left of the single spherical surface as shown in Figure 6.32. The image formed on the other side of the surface is II ‘ . Consider a ray from O’ in the first medium towards C in the second medium. As this ray is incident normal to the spherical surface, it goes undeviated in the second medium.The position of image may be located using the Equation (6.60).

The lateral or transverse magnification m is defined as the ratio of height of the image to the height of the object.

From the two similar triangles ∆ COO’ and ∆ CII ' , we can write,

Applying sign conventions in the above equation (6.59),

II ′ = −h₂ , OO′ = h₁ , PI = +v,

PC = +R, PO = −u

Where, h₁ is the height of the object and h₂ is the height of the image.

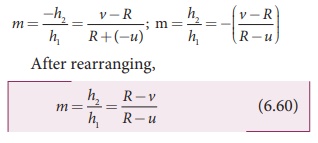
We can also arrive at an equation for lateral magnification involving the refractive indices of the two media.

Let us consider the equation for single spherical surface as,

Substituting equations (6.61) and (6.62) in equation (6.60) we get the equation for lateral magnification as,

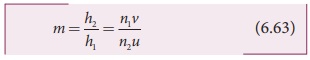
EXAMPLE 6.13

Find the size of the image formed in the given figure.

Solution

Given, u = –40 cm, R = –20 cm, n₁ = 1 and n₂ = 1.33

Equation for single spherical surface is,

= 0.6cm (or) h = 0.6cm

The erect virtual image of height 0.6 cm is formed at 32.0 cm to the left of the single spherical surface.