Refraction in glass slab

Refraction in glass slab

When a ray of light passes through a glass slab it refracts at two refracting surfaces. When the light ray enters the slab it travels from rarer medium (air) to denser medium (glass). This results  in deviation of ray towards the normal. When the light ray leaves the slab it travels from denser medium to rarer medium resulting in deviation of ray away from the normal. After the two refractions, the emerging ray has the same direction as that of the incident ray on the slab with a lateral displacement or shift L. i.e. There is no change in the direction of ray but the path of the incident ray and refracted ray are different and parallel to each other. To calculate the lateral displacement, a perpendicular is drawn in between the paths of incident ray and refracted ray as shown in Figure 6.30.

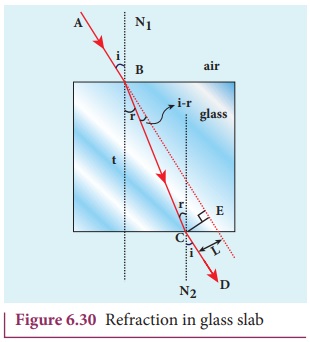
Consider a glass slab of thickness t and  refractive index n is kept in air medium. The path of the light is ABCD and the refractions occur at two points B and C in the glass slab. The angles of incidence i and refraction r are measured with respect to the normal N₁ and N₂ at the two points B and C respectively. The lateral displacement L is the perpendicular distance CE drawn between the path of light and the undeviated path of light at point C.

In the right angle triangle ∆BCE,

In the right angle triangle ∆BCF,

Equating equations (6.48) and (6.49),

Lateral displacement depends upon the thickness of the slab. Thicker the slab, greater will be the lateral displacement. Greater the angle of incident, larger will be the lateral displacement.

EXAMPLE 6.11

The thickness of a glass slab is 0.25 m. it has a refractive index of 1.5. A ray of light is incident on the surface of the slab at an angle of 60º. Find the lateral displacement of the light when it emerges from the other side of the mirror.

Solution

Given, thickness of the slab, t = 0.25 m, refractive index, n = 1.5, angle of incidence, i = 60º.

Using Snell’s law, 1 × sin i = n sin r

sinr = sini / n = sin60 / 1.5  = 0.58

r = sin⁻¹ 0.58 = 35.25º

The lateral displacement is, L = 12.81 cm