Propositional and Predicate Logic

Propositional and Predicate Logic

Logic is concerned with reasoning and the validity of arguments. In general, in logic, we are not concerned with the truth of statements, but rather with their validity. That is to say, although the following argument is clearly logical, it is not something that we would consider to be true:

All lemons are blue

Mary is a lemon

Therefore, Mary is blue

This set of statements is considered to be valid because the conclusion (Mary is blue) follows logically from the other two statements, which we often call the premises. The reason that validity and truth can be separated in this way is simple: a piece of a reasoning is considered to be valid if its conclusion is true in cases where its premises are also true. Hence, a valid set of statements such as the ones above can give a false conclusion, provided one or more of the premises are also false.

We can say: a piece of reasoning is valid if it leads to a true conclusion in every situation where the premises are true.

Logic is concerned with truth values. The possible truth values are true and false. These can be considered to be the fundamental units of logic, and almost all logic is ultimately concerned with these truth values.

Logic is widely used in computer science, and particularly in Artificial Intelligence. Logic is widely used as a representational method for Artificial Intelligence. Unlike some other representations, logic allows us to easily reason about negatives (such as, “this book is not red”) and disjunctions (“or”—such as, “He’s either a soldier or a sailor”).

Logic is also often used as a representational method for communicating concepts and theories within the Artificial Intelligence community. In addition, logic is used to represent language in systems that are able to understand and analyze human language.

As we will see, one of the main weaknesses of traditional logic is its inability to deal with uncertainty. Logical statements must be expressed in terms of truth or falsehood—it is not possible to reason, in classical logic, about possibilities. We will see different versions of logic such as modal logics that provide some ability to reason about possibilities, and also probabilistic methods and fuzzy logic that provide much more rigorous ways to reason in uncertain situations.

Logical Operators

In reasoning about truth values, we need to use a number of operators, which can be applied to truth values.

We are familiar with several of these operators from everyday language:

I like apples and oranges.

You can have an ice cream or a cake.

If you come from France, then you speak French.

Here we see the four most basic logical operators being used in everyday language. The operators are:

and

or

not

if . . . then . . . (usually called implies)

One important point to note is that or is slightly different from the way we usually use it. In the sentence, “You can have an icecream or a cake,” the mother is usually suggesting to her child that he can only have one of the items, but not both. This is referred to as an exclusive-or in logic because the case where both are allowed is excluded.

The version of or that is used in logic is called inclusive-or and allows the case with both options.

The operators are usually written using the following symbols, although other

symbols are sometimes used, according to the context: and ∧

or ∨

not ￢

implies →

iff ↔

Iff is an abbreviation that is commonly used to mean “if and only if.”

We see later that this is a stronger form of implies that holds true if one thing implies another, and also the second thing implies the first.

For example, “you can have an ice-cream if and only if you eat your dinner.” It may not be immediately apparent why this is different from “you can have an icecream if you eat your dinner.” This is because most mothers really mean iff when they use if in this way.

Translating between English and Logic Notation

To use logic, it is first necessary to convert facts and rules about the real world into logical expressions using the logical operators

Without a reasonable amount of experience at this translation, it can seem quite a

daunting task in some cases.

Let us examine some examples. First, we will consider the simple operators, ∧, ∨, and

￢.

Sentences that use the word and in English to express more than one concept, all of which is true at once, can be easily translated into logic using the AND operator, ∧.

For example: “It is raining and it is Tuesday.” might be expressed as: R ∧ T, Where R means “it is raining” and T means “it is Tuesday.”

For example, if it is not necessary to discuss where it is raining, R is probably enough. If we need to write expressions such as “it is raining in New York” or “it is raining heavily” or even “it rained for 30 minutes on Thursday,” then R will probably not suffice. To express more complex concepts like these, we usually use predicates. Hence, for example, we might translate “it is raining in New York” as: N(R) We

might equally well choose to write it as: R(N)

This depends on whether we consider the rain to be a property of New York, or vice versa. In other words, when we write N(R), we are saying that a property of the rain is that it is in New York, whereas with R(N) we are saying that a property of New York is that it is raining. Which we use depends on the problem we are solving. It is likely that if we are solving a problem about New York, we would use R(N), whereas if we are solving a problem about the location of various types of weather, we might use N(R).

Let us return nowto the logical operators. The expression “it is raining inNew York, and I’meither getting sick or just very tired”can be expressed as follows: R(N) ∧ (S(I) ∨ T(I))

Here we have used both the ∧ operator, and the ∨ operator to express a collection of statements. The statement can be broken down into two sections, which is indicated by the use of parentheses.

The section in the parentheses is S(I) ∨ T(I), which means “I’m either getting sick OR I’m very tired”. This expression is “AND’ed”with the part outside the parentheses, which is R(N).

Finally, the ￢ operator is applied exactly as you would expect—to express negation. For example, It is not raining in New York, might be expressed as ￢R(N)

It is important to get the ￢ in the right place. For example: “I’m either not well or just very tired” would be translated as ￢W(I) ∨ T(I)

The position of the ￢ here indicates that it is bound to W(I) and does not play any

role in affecting T(I).

Now let us see how the → operator is used. Often when dealing with logic we are discussing rules, which express concepts such as “if it is raining then I will get wet.”

This sentence might be translated into logic as R→W(I)

This is read “R implies W(I)” or “IF R THEN W(I)”. By replacing the symbols R and W(I) with their respective English language equivalents, we can see that this sentence can be read as “raining implies I’ll get wet” or “IF it’s raining THEN I’ll get wet.”

Implication can be used to express much more complex concepts than this.

For example, “Whenever he eats sandwiches that have pickles in them, he ends up either asleep at his desk or singing loud songs” might be translated as S(y) ∧ E(x, y) ∧ P(y)→A(x) ∨ (S(x, z) ∧ L(z))

Here we have used the following symbol translations:  S(y) means that y is a sandwich. E(x, y) means that x (the man) eats y (the sandwich).

P(y) means that y (the sandwich) has pickles in it.

A(x) means that x ends up asleep at his desk.

S(x, z) means that x (the man) sings z (songs).  L(z) means that z (the songs) are loud.

The important thing to realize is that the choice of variables and predicates is important, but that you can choose any variables and predicates that map well to your problem and that help you to solve the problem.

For example, in the example we have just looked at, we could perfectly well have used instead S→A ∨ L where S means “he eats a sandwich which has pickles in it,” A means “he ends up asleep at his desk,” and L means “he sings loud songs.”

The choice of granularity is important, but there is no right or wrong way to make this choice. In this simpler logical expression, we have chosen to express a simple relationship between three variables, which makes sense if those variables are all that we care about—in other words, we don’t need to know anything else about the sandwich, or the songs, or the man, and the facts we examine are simply whether or not he eats a sandwich with pickles, sleeps at his desk, and sings loud songs.

The first translation we gave is more appropriate if we need to examine these concepts in more detail and reason more deeply about the entities involved.

Note that we have thus far tended to use single letters to represent logical variables. It is also perfectly acceptable to use longer variable names, and thus to write expressions such as the following:

Fish (x) ∧ living (x) →has_scales (x)

This kind of notation is obviously more useful when writing logical expressions that are intended to be read by humans but when manipulated by a computer do not add any value.

Truth Tables

We can use variables to represent possible truth values, in much the same way that variables are used in algebra to represent possible numerical values.

We can then apply logical operators to these variables and can reason about the way in which they behave.

It is usual to represent the behavior of these logical operators using truth tables.

A truth table shows the possible values that can be generated by applying an operator to truth values.

Not

First of all, we will look at the truth table for not, ￢.

Not is a unary operator, which means it is applied only to one variable.

Its behavior is very simple:

true is equal to false

false is equal to true

If variable A has value true, then ￢A has value false.

If variable B has value false, then ￢B has value true.

Ø These can be represented by a truth table,

And

Now, let us examine the truth table for our first binary operator—one which acts on two variables:

∧ is also called the conjunctive operator.

A ∧ B is the conjunction of A and B.

You can see that the only entry in the truth table for which A ∧ B is true is the

one where A is true and B is true. If A is false, or if B is false, then A ∧ B is false. If both A and B are false, then A ∧ B is also false.

What do A and B mean? They can represent any statement, or proposition, that can take on a truth value.

For example, A might represent “It’s sunny,” and B might represent “It’s warm outside.” In this case, A ∧ B would mean “It is sunny and it’s warm outside,” which clearly is true only if the two component parts are true (i.e., if it is true that it is sunny and it is true that it is warm outside).

Or

The truth table for the or operator, ∨

∨ is also called the disjunctive operator.

A ∨ B is the disjunction of A and B.

Clearly A ∨ B is true for any situation except when both A and B are false.

If A is true, or if B is true, or if both A and B are true, A ∨ B is true.

This table represents the inclusive-or operator.

A table to represent exclusive-or would have false in the final row. In other

words, while A ∨ B is true if A and B are both true, A EOR B (A exclusive-or

is false if A and B are both true.

You may also notice a pleasing symmetry between the truth tables for ∧ and ∨. This will become useful later, as will a number of other symmetrical relationships.

Implies

The truth table for implies (→) is a little less intuitive.

This form of implication is also known as material implication

In the statement A→B, A is the antecedent, and B is the consequent. The bottom two lines of the table should be obvious. If A is true and B is true, then A → B seems to be a reasonable thing to believe.

For example, if A means “you live in France” and B means “You speak French,” then A→B corresponds to the statement “if you live in France, then you speak French.”

Clearly, this statement is true (A→B is true) if I live in France and I speak French (A is true and B is true).

Similarly, if I live in France, but I don’t speak French (A is true, but B is false), then it is clear that A→B is not true.

The situations where A is false are a little less clear. If I do not live in France (A is not true), then the truth table tells us that regardless of whether I speak French or not (the value of B), the statement A→B is true. A→B is usually read as “A implies B” but can also be read as “If A then B” or “If A is true then B is true.”

Hence, if A is false, the statement is not really saying anything about the value of B, so B is free to take on any value (as long as it is true or false, of course!).

All of the following statements are valid:

52 = 25 →4 = 4 (true →true)

9 _ 9 = 123 →8 > 3 (false →true)

52 = 25 →0 = 2 (false →false)

In fact, in the second and third examples, the consequent could be given any meaning, and the statement would still be true. For example, the following statement is valid:

52 = 25 →Logic is weird

Notice that when looking at simple logical statements like these, there does not need to be any real-world relationship between the antecedent and the consequent.

For logic to be useful, though, we tend to want the relationships being expressed to be meaningful as well as being logically true.

Iff

Ø The truth table for iff (if and only if {↔}) is as follows:

It can be seen that A ↔ B is true as long as A and B have the same value.

In other words, if one is true and the other false, then A ↔ B is false. Otherwise, if A and B have the same value, A↔ B is true.

Complex Truth Tables

Truth tables are not limited to showing the values for single operators.

For example, a truth table can be used to display the possible values for A ∧ (B ∨C).

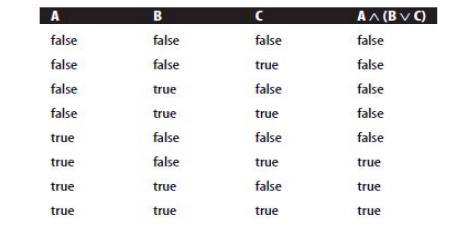
Note that for two variables, the truth table has four lines, and for three variables, it has

eight. In general, a truth table for n variables will have 2ⁿ lines.

The use of brackets in this expression is important. A ∧ (B ∨ C) is not the same as (A ∧ B) ∨ C.

To avoid ambiguity, the logical operators are assigned precedence, as with mathematical operators.

The order of precedence that is used is as follows: ￢, ∧, ∨,→,↔

Hence, in a statement such as ￢A ∨ ￢B ∧ C, the ￢ operator has the greatest

precedence, meaning that it is most closely tied to its symbols. ∧ has a greater precedence than ∨, which means that the sentence above can be expressed as (￢A) ∨ ((￢B) ∧ C)

Similarly, when we write ￢A ∨ B this is the same as (￢A) ∨ B rather than ￢(A ∨ B)

In general, it is a good idea to use brackets whenever an expression might otherwise be ambiguous.

Tautology

Consider the following truth table:

This truth table has a property that we have not seen before: the value of the expression A∨￢A is true regardless of the value of A.

An expression like this that is always true is called a tautology. If A is a tautology, we write: |=A

A logical expression that is a tautology is often described as being valid.

A valid expression is defined as being one that is true under any interpretation.

In other words, no matter what meanings and values we assign to the variables in a valid expression, it will still be true.

For example, the following sentences are all valid:

If wibble is true, then wibble is true.

Either wibble is true, or wibble is not true.

In the language of logic, we can replace wibble with the symbol A, in which case these two statements can be rewritten as

A→A

∨ ￢A

If an expression is false in any interpretation, it is described as being contradictory. The following expressions are contradictory:

∧ ￢A

(A ∨ ￢A)→(A ∧ ￢A)

Equivalence

Consider the following two expressions: A ∧ B

B ∧ A

It should be fairly clear that these two expressions will always have the same value for a given pair of values for A and B.

In otherwords, we say that the first expression is logically equivalent to the second

expression.

We write this as A ∧ B _ B ∧ A. This means that the ∧ operator is commutative.

Note that this is not the same as implication: A ∧ B→B ∧ A, although this second statement is also true.

The difference is that if for two expressions e1 and e2: e1 _ e2, then e1 will always have the same value as e2 for a given set of variables.

On the other hand, as we have seen, e1→e2 is true if e1 is false and e2 is true. There are a number of logical equivalences that are extremely useful.

The following is a list of a few of the most common:

A ∨ A _ A

A ∧ A _ A

A ∧ (B ∧ C) _ (A ∧ B) ∧ C (∧ is associative)

A ∨ (B ∨ C) _ (A ∨ B) ∨ C (∨ is associative)

A ∧ (B ∨ C) _ (A ∧ B) ∨ (A ∧ C) (∧ is distributive over ∨ )

A ∧ (A ∨ B) _ A

A ∨ (A ∧ B) _ A

A ∧ true _ A

A ∧ false _ false

A ∨ true _ true

A ∨ false _ A

All of these equivalences can be proved by drawing up the truth tables for each side of the equivalence and seeing if the two tables are the same.

The following is a very important equivalence: A→B _ ￢A ∨ B

We do not need to use the → symbol at all—we can replace it with a combination of ￢ and ∨ .

Similarly, the following equivalences mean we do not need to use ∧ or↔:

A ∧ B _ ￢(￢A ∨ ￢B)

A↔ B _ ￢(￢(￢A ∨ B) ∨ ￢ (￢B ∨ A))

In fact, any binary logical operator can be expressed using ￢ and ∨ . This is a fact

that is employed in electronic circuits, where nor gates, based on an operator called nor, are used. Nor is represented by ↓, and is defined as follows:

A ↓ B _ ￢(A ∨ B)

Finally, the following equivalences are known as DeMorgan’s Laws:

A ∧ B _ ￢(￢A ∨ ￢B)

A ∨ B _ ￢(￢A ∧ ￢B)

By using these and other equivalences, logical expressions can be simplified.

For example, (C ∧ D) ∨ ((C ∧ D) ∧ E) can be simplified using the following rule: A ∨ (A ∧ B) _ A hence, (C ∧ D) ∨ ((C ∧ D) ∧ E) _ C ∧ D

In this way, it is possible to eliminate subexpressions that do not contribute to the overall value of the expression.

Propositional Logic

There are a number of possible systems of logic.

The system we have been examining so far is called propositional logic.

The language that is used to express propositional logic is called the propositional calculus.

A logical system can be defined in terms of its syntax (the alphabet of symbols and how they can be combined), its semantics (what the symbols mean), and a set of rules of deduction that enable us to derive one expression from a set of other expressions and thus make arguments and proofs.

Syntax

We have already examined the syntax of propositional calculus. The alphabet of symbols, _ is defined as follows

= {true, false, ￢,→, (, ), ∧, ∨ ,↔, p1, p2, p3, . . . , pn, . . . }

Here we have used set notation to define the possible values that are contained within the alphabet ∑.

Note that we allow an infinite number of proposition letters, or propositional symbols, p1, p2, p3, . . . , and so on.

More usually, we will represent these by capital letters P, Q, R, and so on,

If we need to represent a very large number of them, we will use the subscript notation (e.g., p1).

An expression is referred to as a well-formed formula (often abbreviated as wff) or a sentence if it is constructed correctly, according to the rules of the syntax of propositional calculus, which are defined as follows.

In these rules, we use A, B, C to represent sentences. In other words, we define a sentence recursively, in terms of other sentences.

The following are wellformed sentences:

P,Q,R. . .

true, false

(A)

￢A

A ∧ B

A ∨ B

A→B

A↔ B

Hence, we can see that the following is an example of a wff: P ∧ Q ∨ (B ∧ ￢C)→A ∧ B ∨ D ∧ (￢E)