Chapter: Artificial Intelligence
Probabilistic Reasoning
Probabilistic Reasoning
Probability theory is used to discuss events,
categories, and hypotheses about which there is not 100% certainty.
We might write AŌåÆB, which means that if A is true,
then B is true. If we are unsure whether A is true, then we cannot make use of
this expression.
In many real-world situations, it is very useful to
be able to talk about things that lack certainty. For example, what will the
weather be like tomorrow? We might formulate a very simple hypothesis based on
general observation, such as ŌĆ£it is sunny only 10% of the time, and rainy 70%
of the timeŌĆØ. We can use a notation similar to that used for predicate calculus
to express such statements:
P(S) = 0.1
P(R) = 0.7
The first of these statements says that the
probability of S (ŌĆ£it is sunnyŌĆØ) is 0.1. The second says that the probability
of R is 0.7. Probabilities are always expressed as real numbers between 0 and
1. A probability of 0 means ŌĆ£definitely notŌĆØ and a probability of 1 means
ŌĆ£definitely so.ŌĆØ Hence, P(S) = 1 means that it is always sunny.
Many of the operators and notations that are used
in prepositional logic can also be used in probabilistic notation. For example,
P(’┐óS) means ŌĆ£the probability that it is
not sunnyŌĆØ; P(S Ōł¦ R) means ŌĆ£the probability that it is both sunny
and rainy.ŌĆØ P(A Ōł© B),
which means ŌĆ£the probability that either A is true or B is true,ŌĆØ is defined by
the following rule: P(A Ōł© B) =
P(A) + P(B) - P(A Ōł¦ B)
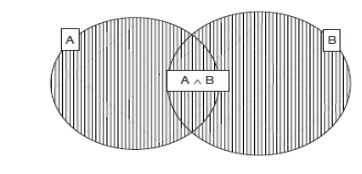
The notation P(B|A) can be read as ŌĆ£the probability
of B, given A.ŌĆØ This is known as conditional probabilityŌĆöit is conditional on
A. In other words, it states the probability that B is true, given that we
already know that A is true. P(B|A) is defined by the following rule: Of
course, this rule cannot be used in cases where P(A) = 0.
For example, let us suppose that the likelihood
that it is both sunny and rainy at the same time is 0.01. Then we can calculate
the probability that it is rainy, given that it is sunny as follows:

The basic approach statistical methods adopt to
deal with uncertainty is via the axioms of probability:
Probabilities are (real) numbers in the range 0 to
1.
A probability of P(A) = 0 indicates total
uncertainty in A, P(A)
= 1 total certainty and values in between some degree of (un)certainty.
Probabilities can be calculated in a number of
ways.
Probability = (number of desired outcomes) / (total
number of outcomes)
So given a pack of playing cards the probability of
being dealt an ace from a full normal deck is 4 (the number of aces) / 52
(number of cards in deck) which is 1/13. Similarly the probability of being
dealt a spade suit is 13 / 52 = 1/4.
If you have a choice of number of items k from a set of items n then the

Conditional probability, P(A|B), indicates the probability of of event A given that we know event B
has occurred.
A Bayesian
Network is a directed acyclic graph:
A graph where the directions are links which
indicate dependencies that exist between nodes.
Nodes represent propositions about events or events
themselves.
Conditional probabilities quantify the strength of
dependencies.
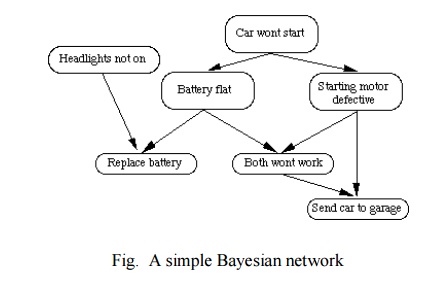
Consider the following example:
If my car won't start then it is likely that
The battery is flat or
The staring motor is broken.
In order to decide whether to fix the car myself or
send it to the garage I make the following decision:
If the headlights do not work then the battery is
likely to be flat so i fix it
myself.
If the starting motor is defective then send car to
garage.
If battery and starting motor both gone send car to
garage. The network to represent this is as follows:
Bayesian probabilistic inference
BayesŌĆÖ theorem can be used to calculate the probability that a certain event will occur or that a certain proposition is true
The theorem is stated as follows:
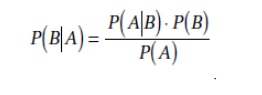
P(B) is called the prior probability of B. P(B|A), as well as being called the conditional probability, is also known as the posterior probability of B.
P(A Ōł¦ B) = P(A|B)P(B)
Note that due to the commutativity of Ōł¦, we can also write
P(A Ōł¦ B) = P(B|A)P(A)
Hence, we can deduce: P(B|A)P(A) = P(A|B)P(B)
This can then be rearranged to give BayesŌĆÖ theorem:

The set of all hypotheses must be mutually exclusive and exhaustive.
Thus to find if we examine medical evidence to diagnose an illness. We must know all the prior probabilities of find symptom and also the probability of having an illness based on certain symptoms being observed.
Bayesian statistics lie at the heart of most statistical reasoning systems. How is Bayes theorem exploited?
The key is to formulate problem correctly:
P(A|B) states the probability of A given only B's evidence. If there is other relevant evidence then it must also be considered.
All events must be mutually exclusive. However in real world problems events are not generally unrelated. For example in diagnosing measles, the symptoms of spots and a fever are related. This means that computing the conditional probabilities gets complex.
In general if a prior evidence, p and some new observation, N then
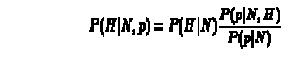
computing grows exponentially for large sets of p
All events must be exhaustive. This means that in order to compute all probabilities the set of possible events must be closed. Thus if new information arises the set must be created afresh and all probabilities recalculated.
Thus Simple Bayes rule-based systems are not suitable for uncertain reasoning.
Knowledge acquisition is very hard.
Too many probabilities needed -- too large a storage space.
Computation time is too large.
Updating new information is difficult and time consuming.
Exceptions like ``none of the above'' cannot be represented.
Humans are not very good probability estimators.
However, Bayesian statistics still provide the core to reasoning in many uncertain reasoning systems with suitable enhancement to overcome the above problems. We will look at three broad categories:
Certainty factors
Dempster-Shafer models
Bayesian networks.
Bayesian networks are also called Belief Networks or Probabilistic Inference Networks.
Related Topics