Password Management

PASSWORD MANAGEMENT

1. Password Protection

The front line of defense against intruders is the password system. Virtually all multiuser systems require that a user provide not only a name or identifier (ID) but also a password. The password serves to authenticate the ID of the individual logging on to the system. In turn, the ID provides security in the following ways:

·       The ID determines whether the user is authorized to gain access to a system.  

·        The ID determines the privileges accorded to the user.  

·        The ID is used in ,what is referred to as discretionary access control. For example, by listing the IDs of the other users, a user may grant permission to them to read files owned by that user.  

2. The Vulnerability of Passwords

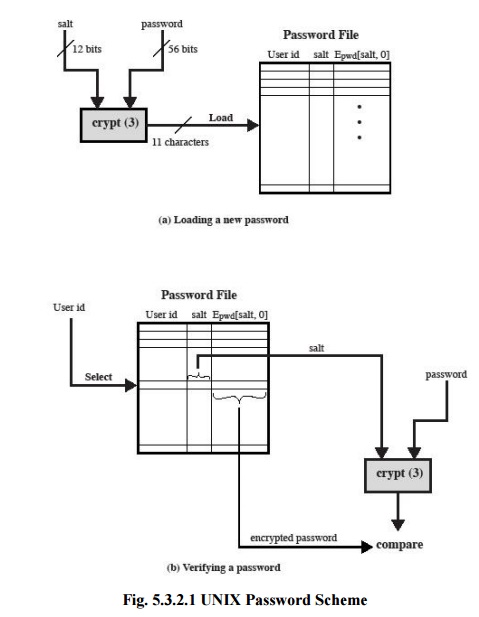
To understand the nature of the threat to password-based systems, let us consider a scheme that is widely used on UNIX, the following procedure is employed.

^·         Each user selects a password of up to eight printable characters in length.  

^·         This is converted into a 56-bit value (using 7-bit ASCII) that serves as the key input to an encryption routine.  

·        The encryption routine, known as crypt(3), is based on DES. The DES algorithm is modified using a 12-bit "salt" value.

^·         Typically, this value is related to the time at which the password is assigned to the user.  

^·         The modified DES algorithm is exercised with a data input consisting of a 64-bit block of zeros.

^·         The output of the algorithm then serves as input for a second encryption.  

^·         This process is repeated for a total of 25 encryptions.  

^·         The resulting 64-bit output is then translated into an 11-character sequence.  

^·         The hashed password is then stored, together with a plaintext copy of the salt, in the password file for the corresponding user ID.  

^·         This method has been shown to be secure against a variety of cryptanalytic attacks  

The salt serves three purposes:

·        It prevents duplicate passwords from being visible in the password file. Even if two users choose the same password, those passwords will be assigned at different times. Hence, the "extended" passwords of the two users will differ.  

·        It effectively increases the length of the password without requiring the user to remember two additional characters.  

·        It prevents the use of a hardware implementation of DES, which would ease the difficulty of a brute-force guessing attack.  

When a user attempts to log on to a UNIX system, the user provides an ID and a password. The operating system uses the ID to index into the password file and retrieve the plaintext salt and the encrypted password. The salt and user-supplied password are used as input to the encryption routine. If the result matches the stored value, the password is accepted.The encryption routine is designed to discourage guessing attacks. Software implementations of DES are slow compared to hardware versions, and the use of 25 iterations multiplies the time required by 25.

Thus, there are two threats to the UNIX password scheme. First, a user can gain access on a machine using a guest account or by some other means and then run a password guessing program, called a password cracker, on that machine.

As an example, a password cracker was reported on the Internet in August 1993. Using a Thinking Machines Corporation parallel computer, a performance of 1560 encryptions per second per vector unit was achieved. With four vector units per processing node (a standard configuration), this works out to 800,000 encryptions per second on a 128-node machine (which is a modest size) and 6.4 million encryptions per second on a 1024-node machine.

Password length is only part of the problem. Many people, when permitted to choose their own password, pick a password that is guessable, such as their own name, their street name, a common dictionary word, and so forth. This makes the job of password cracking straightforward.

Following strategy was used:

Try the user's name, initials, account name, and other relevant personal information. In all, 130 different permutations for each user were tried.

Try words from various dictionaries.

Try various permutations on the words from step 2.

Try various capitalization permutations on the words from step 2 that were not considered in step 3. This added almost 2 million additional words to the list.

3. Access Control

One way to thwart a password attack is to deny the opponent access to the password file. If the encrypted password portion of the file is accessible only by a privileged user, then the opponent cannot read it without already knowing the password of a privileged user.

Password Selection Strategies

Four basic techniques are in use:

·  User education  

·  Computer-generated passwords  

· Reactive password checking   

· Proactive password checking  

Users can be told the importance of using hard-to-guess passwords and can be provided with guidelines for selecting strong passwords. This user education strategy is unlikely to succeed at most installations, particularly where there is a large user population or a lot of turnover. Many users will simply ignore the guidelines

Computer-generated passwords also have problems. If the passwords are quite random in nature, users will not be able to remember them. Even if the password is pronounceable, the user may have difficulty remembering it and so be tempted to write it down

A reactive password checking strategy is one in which the system periodically runs its own password cracker to find guessable passwords.

The most promising approach to improved password security is a proactive password checker. In this scheme, a user is allowed to select his or her own password. However, at the time of selection, the system checks to see if the password is allowable and, if not, rejects it. Such checkers are based on the philosophy that, with sufficient guidance from the system, users can select memorable passwords from a fairly large password space that are not likely to be guessed in a dictionary attack.

The first approach is a simple system for rule enforcement. For example, the following rules could be enforced:

·        All passwords must be at least eight characters long.  

·        In the first eight characters, the passwords must include at least one each of uppercase, lowercase, numeric digits, and punctuation marks. These rules could be coupled with advice to the user. Although this approach is superior to simply educating users, it may not be sufficient to thwart password crackers. This scheme alerts crackers as to which passwords not to try but may still make it possible to do password cracking.

Another possible procedure is simply to compile a large dictionary of possible "bad" passwords. When a user selects a password, the system checks to make sure that it is not on the disapproved list.

There are two problems with this approach:

·       Space: The dictionary must be very large to be effective..  

·        Time: The time required to search a large dictionary may itself be large  

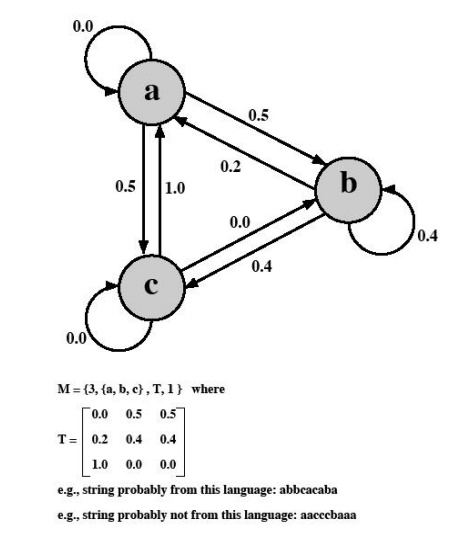
Two techniques for developing an effective and efficient proactive password checker that is based on rejecting words on a list show promise. One of these develops a Markov model for the generation of guessable passwords. This model shows a language consisting of an alphabet of three characters. The state of the system at any time is the identity of the most recent letter. The value on the transition from one state to another represents the probability that one letter follows another. Thus, the probability that the next letter is b, given that the current letter is a, is 0.5.

In general, a Markov model is a quadruple [m, A, T, k], where m is the number of states in the model, A is the state space, T is the matrix of transition probabilities, and k is the order of the model. For a kth-order model, the probability of making a transition to a particular letter depends on the previous k letters that have been generated.

The authors report on the development and use of a second-order model. To begin, a dictionary of guessable passwords is constructed. Then the transition matrix is calculated as follows:

1.     Determine the frequency matrix f, where f(i, j, k) is the number of occurrences of the trigram consisting of the ith, jth, and kth character. For example, the password parsnips yields the trigrams par, ars, rsn, sni, nip, and ips.

2.     For each bigram ij, calculate f(i, j,∞) as the total number of trigrams beginning with ij. For example, f(a, b,∞) would be the total number of trigrams of the form aba, abb, abc, and so on.

3.     Compute the entries of T as follows:

T(i,j,k) = f(i, j, k) / f(i, j,∞)

The result is a model that reflects the structure of the words in the dictionary.

A quite different approach has been reported by Spafford. It is based on the use of a Bloom filter. To begin, we explain the operation of the Bloom filter. A Bloom filter of order k consists of a set of k independent hash functions H₁(x), H₂(x),..., H_k(x), where each function maps a password into a hash value in the range 0 to N - 1 That is,

H_i(X_j) = y 1 ≤i ≤k; 1 ≤j ≤D; 0 ≤y ≤N- 1

where

X_j   = jth word in password dictionary

D   = number of words in password dictionary

The following procedure is then applied to the dictionary:

·        A hash table of N bits is defined, with all bits initially set to 0.

·        For each password, its k hash values are calculated, and the corresponding bits in the hash table are set to 1. Thus, if H_i(X_j) = 67 for some (i, j), then the sixty-seventh bit of the hash table is set to 1; if the bit already has the value 1, it

remains at 1.

When a new password is presented to the checker, its k hash values are calculated. If all the corresponding bits of the hash table are equal to 1, then the password is rejected.