Block Cipher Principles

BLOCK CIPHER PRINCIPLES

Virtually, all symmetric block encryption algorithms in current use are based on a structure referred to as Fiestel block cipher. For that reason, it is important to examine the design principles of the Fiestel cipher. We begin with a comparison of stream cipher with block

cipher.

A stream cipher is one that encrypts a digital data stream one bit or one byte at a time. E.g, vigenere cipher. A block cipher is one in which a block of plaintext is treated as a whole and used to produce a cipher text block of equal length. Typically a block size of 64 or 128 bits is used.

1 Block cipher principles

most symmetric block ciphers are based on a Feistel Cipher Structure

needed since must be able to decrypt ciphertext to recover messages efficiently

block ciphers look like an extremely large substitution

would need table of 264 entries for a 64-bit block

instead create from smaller building blocks

using idea of a product cipher in 1949 Claude Shannon introduced idea of substitution-permutation (S-P) networks called modern substitution-transposition product cipher these form the basis of modern block ciphers

S-P networks are based on the two primitive cryptographic operations we have seen before:

substitution (S-box)

permutation (P-box)

provide confusion and diffusion of message

diffusion – dissipates statistical structure of plaintext over bulk of ciphertext

confusion – makes relationship between ciphertext and key as complex as possible

2 Feistel cipher structure

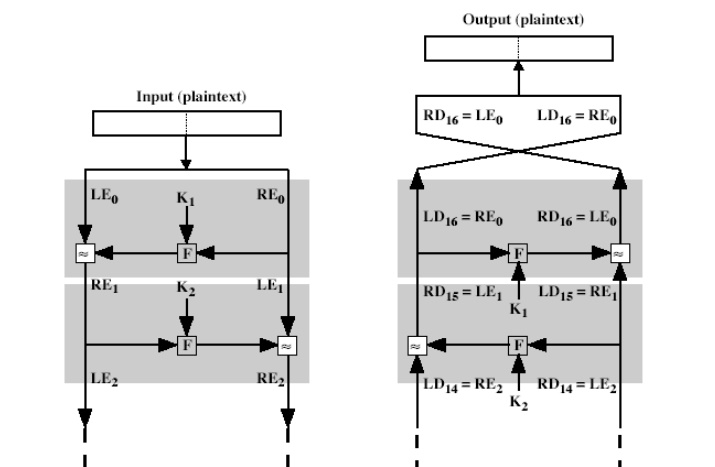
The input to the encryption algorithm are a plaintext block of length 2w bits and a key K. the plaintext block is divided into two halves L₀ and R₀. The two halves of the data pass through „n‟ rounds of processing and then combine to produce the ciphertext block. Each round „i‟ has inputs L_i-1 and R_i-1, derived from the previous round, as well as the subkey K_i, derived from the overall key K. in general, the subkeys K_i are different from K and from each other.

All rounds have the same structure. A substitution is performed on the left half of the data (as similar to S-DES). This is done by applying a round function F to the right half of the data and then taking the XOR of the output of that function and the left half of the data. The round function has the same general structure for each round but is parameterized by the round subkey k_i. Following this substitution, a permutation is performed that consists of the interchange of the two halves of the data. This structure is a particular form of the substitution-permutation network.

The exact realization of a Feistel network depends on the choice of the following parameters and design features:

Block size - Increasing size improves security, but slows cipher  

Key size - Increasing size improves security, makes exhaustive key searching harder, but may slow cipher  

Number of rounds - Increasing number improves security, but slows cipher  

Subkey generation - Greater complexity can make analysis harder, but slows cipher  

Round function - Greater complexity can make analysis harder, but slows cipher  

Fast software en/decryption & ease of analysis - are more recent concerns for practical use and testing.

The process of decryption is essentially the same as the encryption process. The rule is as follows: use the cipher text as input to the algorithm, but use the subkey k_i in reverse order. i.e., k_n in the first round, k_n-1 in second round and so on. For clarity, we use the notation LE_i and RE_i for data traveling through the decryption algorithm. The diagram below indicates that, at each round, the intermediate value of the decryption process is same (equal) to the corresponding value of the encryption process with two halves of the value swapped.

i.e., RE_i || LE_i (or) equivalently RD_16-i || LD_16-i

After the last iteration of the encryption process, the two halves of the output are swapped, so that the cipher text is RE₁₆ || LE₁₆. The output of that round is the cipher text. Now take the cipher text and use it as input to the same algorithm. The input to the first round is RE₁₆ || LE_16, which is equal to the 32-bit swap of the output of the sixteenth round of the encryption process.

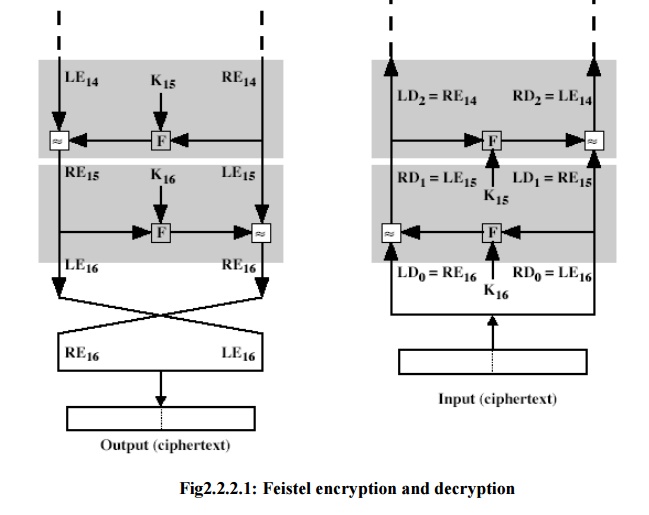
Now we will see how the output of the first round of the decryption process is equal to a 32-bit swap of the input to the sixteenth round of the encryption process. First consider the encryption process,

LE₁₆ = RE₁₅

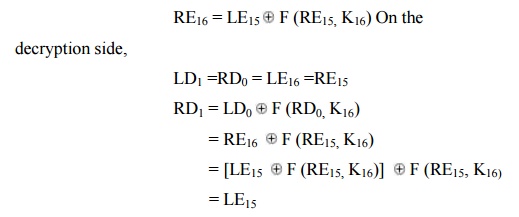
Therefore,            LD₁ = RE₁₅ RD₁ =

LE₁₅

In general, for the i^th iteration of the encryption algorithm,

LE_i = RE_i-1

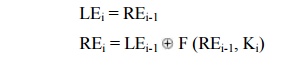
Finally, the output of the last round of the decryption process is RE₀ || LE₀. A 32-bit swap recovers the original plaintext.