Introduction to Number Theory

INTRODUCTION TO NUMBER THEORY

1 Primality Testing and RSA

The first stage of key-generation for RSA involves finding two large primes p, q

Because of the size of numbers used, must find primes by trial and error

Modern primality tests utilize properties of primes eg:

a^n-1 = 1 mod n where GCD(a,n)=1

all primes numbers 'n' will satisfy this equation

some composite numbers will also satisfy the equation, and are called pseudo-primes.

Most modern tests guess at a prime number 'n', then take a large number (eg 100) of numbers 'a', and apply this test to each. If it fails the number is composite, otherwise it is is probably prime.

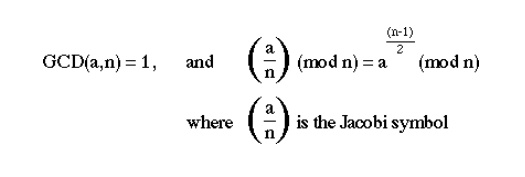
There are a number of stronger tests which will accept fewer composites as prime than the above test. eg:

RSA Implementation in Practice

Software implementations

generally perform at 1-10 bits/second on block sizes of 256-512 bits

two main types of implementations:

- on micros as part of a key exchange mechanism in a hybrid scheme

- on larger machines as components of a secure mail system

Harware Implementations

generally perform 100-10000 bits/sec on blocks sizes of 256-512 bits

all known implementations are large bit length conventional ALU units

2 Euler Totient Function [[phi]](n)

if consider arithmetic modulo n, then a reduced set of residues is a subset of the complete set of residues modulo n which are relatively prime to n

eg for n=10,

the complete set of residues is {0,1,2,3,4,5,6,7,8,9} o the reduced set of residues is {1,3,7,9}

the  number  of  elements  in  the  reduced  set  of  residues  is  called  the  Euler Totient function [[phi]](n)

there is no single formula for [[phi]](n) but for various cases count how many elements are excluded:

p (p prime)         [[phi]](p) =p-1

pr (p prime)       [[phi]](p) =pr-1(p-1)

p.q (p,q prime)   [[phi]](p.q) =(p-1)(q-1)

several important results based on [[phi]](n) are:

Theorem (Euler's Generalization)

let gcd(a,n)=1 then

_a[[phi]](n) _{mod n = 1}

Fermat's Theorem

let p be a prime and gcd(a,p)=1 then

a^p-1 mod p = 1

Algorithms to find Inverses a^-1 mod n

search 1,...,n-1 until an a^-1 is found with a.a^-1 mod n

if [[phi]](n) is known, then from Euler's Generalization

_a-1 _{= a}[[phi]](n)-1 _{mod n}

3.      otherwise use Extended Euclid's algorithm for inverse

3 Computing with Polynomials in GF(qn)

have seen arithmetic modulo a prime number GF(p)

also can do arithmetic modulo q over polynomials of degree n, which also form a Galois

Field GF(qⁿ)

its elements are polynomials of degree (n-1) or lower

a(x)=a_n-1x^n-1+a_n-2x^n-2+...+a₁x+a₀

have residues for polynomials just as for integers

p(x)=q(x)d(x)+r(x)

and this is unique if deg[r(x)]<deg[d(x)]

if r(x)=0, then d(x) divides p(x), or is a factor of p(x)

addition in GF(qⁿ) just involves summing equivalent terms in the polynomial modulo q (XOR if q=2)

a(x)+b(x)=(a_n-1+b_n-1)x^n-1+...+(a₁+b₁)x+(a₀+b₀)

Multiplication with Polynomials in GF(qn)

multiplication in GF(qⁿ) involves

multiplying the two polynomials together (cf longhand multiplication; here use shifts & XORs if q=2)

then finding the residue modulo a given irreducible polynomial of degree n

an irreducible polynomial d(x) is a 'prime' polynomial, it has no polynomial divisors other than itself and 1

modulo reduction of p(x) consists of finding some r(x) st: p(x)=q(x)d(x)+r(x)

nb. in GF(2ⁿ) with d(x)=x³+x+1 can do simply by replacing x³ with x+1

eg in GF(2³) there are 8 elements:

0, 1, x, x+1, x², x²+1, x²+x, x²+x+1

with irreducible polynomial d(x)=x³+x+1* arithmetic in this field can be summarised as:

can adapt GCD, Inverse, and CRT algorithms for GF(qⁿ)

[[phi]](p(x)) = 2ⁿ-1 since every poly except 0 is relatively prime to p(x)

arithmetic in GF(qⁿ) can be much faster than integer arithmetic, especially if the irreducible polynomial is carefully chosen

eg a fast implementation of GF(2¹²⁷) exists

has both advantages and disadvantages for cryptography, calculations are faster, as are methods for breaking

RSA and the Chinese Remainder Theorem

a significant improvement in decryption speed for RSA can be obtained by using the Chinese Remainder theorem to work modulo p and q respectively

since p,q are only half the size of R=p.q and thus the arithmetic is much faster

CRT is used in RSA by creating two equations from the decryption calculation:

M = Cd mod R as follows:

M1 = M mod p = (C mod p)d mod (p-1)

M2 = M mod q = (C mod q)d mod (q-1)

then the pair of equations

M = M1 mod p M = M2 mod q has a unique solution by the CRT, given by:

M = [((M2 +q - M1)u mod q] p + M1

where

p.u mod q = 1