Chapter: Cryptography and Network Security
Finite Fields
FINITE FIELDS
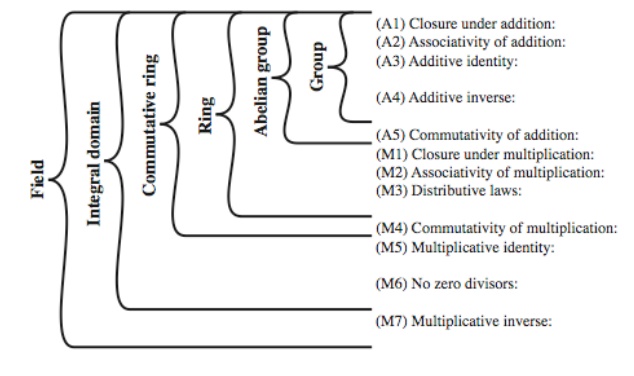
1 Groups, Rings and Field:
Group: A set of elements that is
closed with respect to some operation.
Closed->
The result of the operation is also in the set
The
operation obeys:
Obeys associative law: (a.b).c =
a.(b.c)
Has identity e: e.a = a.e = a
Has inverses a-1: a.a-1 = e
Abelian Group: The operation is commutative
a.b = b.a
Example:
Z8, + modular addition, identity =0
Cyclic Group
Exponentiation:
Repeated application of operator
example: a3 = a.a.a
Cyclic
Group: Every element is a power of some fixed element, i.e., b = ak for some a and every b in group
a is said to be a generator of the group
Example:
{1, 2, 4, 8} with mod 12 multiplication, the generator is 2.
20=1,
21=2, 22=4, 23=8, 24=4, 25=8
Ring:
A group
with two operations: addition and multiplication
The group
is abelian with respect to addition: a+b=b+a
Multiplication
and additions are both associative:
a+(b+c)=(a+b)+c
a.(b.c)=(a.b).c
Multiplication
distributes over addition, a.(b+c)=a.b+a.c
Commutative
Ring: Multiplication is commutative, i.e., a.b
= b.a
Integral
Domain: Multiplication operation has an identity and no zero divisors
Field:
An
integral domain in which each element has a multiplicative inverse.
2 Modular Arithmetic
modular
arithmetic is 'clock arithmetic'
a congruence a = b mod n says when
divided by n that a and b have the
same remainder o 100 = 34 mod 11
usually
have 0<=b<=n-1
-12mod7 =
-5mod7 = 2mod7 = 9mod7 o b is called the residue of a mod n
can do
arithmetic with integers modulo n with all results between 0 and n
Addition
a+b mod n
Subtraction
a-b mod n = a+(-b) mod n
Multiplication
a.b mod n
derived
from repeated addition
can get
a.b=0 where neither a,b=0 o eg 2.5 mod 10
Division
a/b mod n
is
multiplication by inverse of b: a/b = a.b-1 mod n
if n is
prime b-1 mod n exists s.t b.b-1 = 1 mod n o eg 2.3=1 mod 5 hence 4/2=4.3=2
mod 5
integers
modulo n with addition and multiplication form a commutative ring with the laws
of
Associativity : (a+b)+c = a+(b+c) mod n
Commutativity : a+b = b+a mod n
Distributivity : (a+b).c = (a.c)+(b.c) mod n
also can
chose whether to do an operation and then reduce modulo n, or reduce then do
the operation, since reduction is a homomorphism from the ring of integers to
the ring of integers modulo n
a+/-b mod
n = [a mod n +/- b mod n] mod n o (the above laws also hold for multiplication)
if n is
constrained to be a prime number p
then this forms a Galois Field modulo p
denoted GF(p) and all the normal laws
associated with integer arithmetic work
Greatest Common Divisor
the
greatest common divisor (a,b) of a and b is the largest number that divides
evenly into both a and b
Euclid's Algorithm is used
to find the Greatest Common Divisor (GCD) of two numbers a and n, a<n
use fact
if a and b have divisor d so does a-b, a-2b GCD (a,n) is given by:
let g0=n
g1=a
gi+1 =
gi-1 mod gi when gi=0 then (a,n) = gi-1
eg find
(56,98) g0=98 g1=56
g2 = 98
mod 56 = 42
g3 = 56
mod 42 = 14
g4 = 42
mod 14 = 0 hence (56,98)=14
Finite Fields or Galois Fields
Finite
Field: A field with finite number of elements
Also
known as Galois Field
The
number of elements is always a power of a prime number. Hence, denoted as
GF(pn)
GF(p) is
the set of integers {0,1, …, p-1} with arithmetic operations modulo prime p
Can do
addition, subtraction, multiplication, and division without leaving the field
GF(p)
GF(2) =
Mod 2 arithmetic GF(8) = Mod 8 arithmetic
There is
no GF(6) since 6 is not a power of a prime
Polynomial Arithmetic
f(x) = anxn + an-1xn-1 + …+ a1x + a0 = Σ aixi
Ordinary
polynomial arithmetic:
Add, subtract, multiply, divide polynomials,
Find remainders, quotient.
Some polynomials have no factors and are prime.
Polynomial
arithmetic with mod p coefficients
Polynomial
arithmetic with mod p coefficients and mod m(x) operations
Polynomial Arithmetic with Mod 2 Coefficients
All
coefficients are 0 or 1, e.g.,
let f(x)
= x3 + x2 and g(x) = x2
+ x + 1 f(x) + g(x)
= x3 + x + 1
f(x) x
g(x) = x5 + x2
Polynomial
Division: f(x) = q(x) g(x) + r(x)
can
interpret r(x) as being a remainder
r(x) = f(x) mod g(x)
if no
remainder, say g(x) divides f(x)
if g(x)
has no divisors other than itself & 1 say it is irreducible (or prime)
polynomial
Arithmetic
modulo an irreducible polynomial forms a finite field
Can use
Euclid‟s algorithm to find gcd and inverses.
Related Topics