Principles of Public Key Cryptography

PRINCIPLES OF PUBLIC KEY CRYPTOGRAPHY

The concept of public key cryptography evolved from an attempt to attack two of themost difficult problems associated with symmetric encryption.

·        Key distribution under symmetric key encryption requires either (1) that two communicants already share a key, which someone has been distributed to them or (2) the use of a key distribution center.  

·        Digital signatures.  

1. Public key cryptosystems

Public key algorithms rely on one key for encryption and a different but related key for decryption.

These algorithms have the following important characteristics:

·        It is computationally infeasible to determine the decryption key given only the knowledge of the cryptographic algorithm and the encryption key.  

In addition, some algorithms, such as RSA, also exhibit the following characteristic:

·     Either of the two related keys can be used for encryption, with the other used for decryption.

The essential steps are the following:

·        Each user generates a pair of keys to be used for encryption and decryption of messages.  

·        Each user places one of the two keys in a public register or other accessible file. This is the public key. The companion key is kept private.  

·        If A wishes to send a confidential message to B, A encrypts the message using B‟s public key.  

·        When B receives the message, it decrypts using its private key. No other recipient can decrypt the message because only B knows B‟s private key.

With this approach, all participants have access to public keys and private keys are generated locally by each participant and therefore, need not be distributed. As long as a system controls its private key, its incoming communication is secure.

Let the plaintext be X=[X1, X2, X3, …,Xm] where m is the number of letters in some finite alphabets. Suppose A wishes to send a message to B. B generates a pair of keys: a public key KU_b and a private key KR_b. KR_b is known only to B, whereas KU_b is publicly available and therefore accessible by A.

With the message X and encryption key KU_b as input, A forms the cipher text

Y=[Y1, Y2, Y3, … Yn]., i.e., Y=E KU_b(X)

The receiver can decrypt it using the private key KR_b. i.e., X=D KR_b(). The encrypted message serves as a digital signature.

It is important to emphasize that the encryption process just described does not provide confidentiality. There is no protection of confidentiality because any observer can decrypt the message by using the sender‟s public key.

It is however, possible to provide both the authentication and confidentiality by a double use of the public scheme.

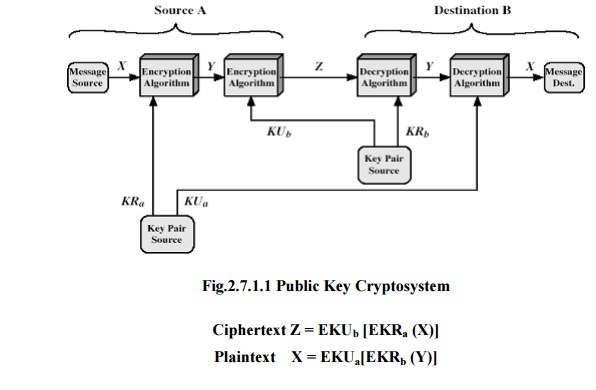
Initially, the message is encrypted using the sender‟s private key. This provides the digital signature. Next, we encrypt again, using the receiver‟s public key. The final ciphertext can be decrypted only by the intended receiver, who alone has the matching private key. Thus confidentiality is provided.

2 Requirements for public key cryptography

It is computationally easy for a party B to generate a pair [KU_b , KR_b].  

It is computationally easy for a sender A, knowing the public key and the message to be encrypted M, to generate the corresponding ciphertext: C=EKU_b(M).  

It is computationally easy for the receiver B to decrypt the resulting ciphertext using the private key to recover the original message: M = DKR_b (C) = DKR_b [EKU_b (M)]  

It is computationally infeasible for an opponent, knowing the public key KU_b, to determine the private key KR_b.  

It is computationally infeasible for an opponent, knowing the public key KU_b, and a ciphertext C, to recover the original message M.  

The encryption and decryption functions can be applied in either order:   M = EKU_b [DKR_b (M) = DKU_b [EKR_b (M)]

Public key cryptanalysis

Public key encryption scheme is vulnerable to a brute force attack. The counter measure is to use large keys.