Modal Logics and Possible Worlds

Modal Logics and Possible Worlds

The forms of logic that we have dealt with so far deal with facts and properties of objects that are either true or false.

In these classical logics, we do not consider the possibility that things change or that things might not always be as they are now.

Modal logics are an extension of classical logic that allow us to reason about possibilities and certainties.

In other words, using a modal logic, we can express ideas such as “although the sky is usually blue, it isn’t always” (for example, at night). In this way, we can reason about possible worlds.

A possible world is a universe or scenario that could logically come about.

The following statements may not be true in our world, but they are possible, in the sense that they are not illogical, and could be true in a possible world:

Trees are all blue.

Dogs can fly.

People have no legs.

It is possible that some of these statements will become true in the future, or even that they were true in the past.

It is also possible to imagine an alternative universe in which these statements are true now.

The following statements, on the other hand, cannot be true in any possible world:

A ∧ ￢A

(x > y) ∧ (y > z) ∧ (z > x)

The first of these illustrates the law of the excluded middle, which simply states that a fact must be either true or false: it cannot be both true and false.

It also cannot be the case that a fact is neither true nor false. This is a law of classical logic, it is possible to have a logical system without the law of the excluded middle, and in which a fact can be both true and false.

The second statement cannot be true by the laws of mathematics. We are not interested in possible worlds in which the laws of logic and mathematics do not hold.

A statement that may be true or false, depending on the situation, is called contingent. A statement that must always have the same truth value, regardless of which possible

world we consider, is noncontingent.

Hence, the following statements are contingent:

A ∧ B

A ∨ B

I like ice cream.

The sky is blue.

The following statements are noncontingent: A ∨ ￢A

A ∧ ￢A

If you like all ice cream, then you like this ice cream.

Clearly, a noncontingent statement can be either true or false, but the fact that it is noncontingent means it will always have that same truth value.

If a statement A is contingent, then we say that A is possibly true, which is written ◊

A

If A is noncontingent, then it is necessarily true, which is written □ A

Reasoning in Modal Logic

It is not possible to draw up a truth table for the operators ◊ and □

The following rules are examples of the axioms that can be used to reason in this kind of modal logic:

□A→◊A

□￢A→￢◊A

◊A→￢□ A

Although truth tables cannot be drawn up to prove these rules, you should be able to reason about them using your understanding of the meaning of the ◊ and □ operators.

Possible world representations

It describes method proposed by Nilsson which generalizes firtst order logic in the modeling of uncertain beliefs

The method assigns truth values ranging from 0 to 1 to possible worlds

Each set of possible worlds corresponds to a different interpretation of sentences contained in a knowledge base denoted as KB

Consider the simple case where a KB contains only the single sentence S, S may be either true or false. We envision S as being true in one set of possible worlds W₁ and false in another set W₂ . The actual world , the one we are in, must be in one of the

two sets, but we are uncertain which one. Uncertainty is expressed by assigning a probability P to W₁ and 1 – P to W_2. We can say then that the probability of S being true is P

When KB contains L sentences, S_1,… S_L , more sets of possible worlds are required to represent all consistent truth value assignments. There are 2^L possible truth assignments for L sentences.

Truth Value assignments for the set {P. P→Q, Q}

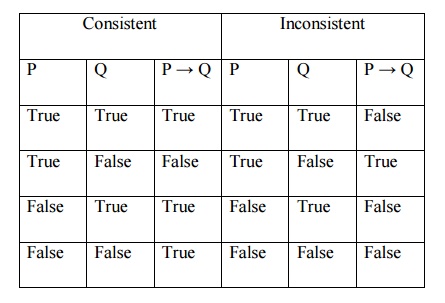
They are based on the use of the probability constraints

0 ≤ p_i ≤ 1, and ∑_i p_i = 1

The consistent probability assignments are bounded by the hyperplanes of a certain convex hull