Homogeneous Functions and Euler’s Theorem

Homogeneous Functions and Euler’s Theorem

Definition 8.12

(a) Let A = {( x, y ) | a < x < b, c < y < d } ⊂ ℝ² , F : A → ℝ, we say that F is a homogeneous function on A , if there exists a constant p such that F ( λ x, λ y ) = λ ^p F ( x , y) for all λ ∈ ℝ and sutitably restricted λ, x, y, such that (λ x , λ y) ∈ A . This constant p is called degree of F .

(b) Let B = {( x, y , z) | a < x < b , c < y < d, u < z < v} ⊂ ℝ³ , G : B → ℝ, we say that G is a homogeneous function on B , if there exists a constant p such that G ( λ x, λ y , λ z ) = λ ^pG ( x, y , z) for all λ ∈ ℝ and sutitably restricted λ, x, y, z, such that (λ x , λ y, λz ) ∈ B . This constant p is called degree of G .

Note: Division by any variable may occur, to avoid division by zero, we say that λ, x, y, z are sutitably restricted real numbers.

These types of functions are important in Ordinary differential equations (Chapter 10). Let us consider some examples.

Consider F ( x, y) = x³ − 2 y³ + 5xy² , (x , y) ∈ ℝ² . Then

F ( λ x , λ y) = (λ x ) ³ − 2(λ y)³ + 5(λ x )(λ y)² = λ³ (x ³ − 2 y³ + 5xy² )

and hence F is a homogeneous function of degree 3.

On the other hand,

G ( x, y) = e^x2 + 3y² is not a homogeneous function

because, G ( λ x , λ y) = e ^(λx)2  + 3(λ y)² ≠ λpG ( x, y)

for any λ ≠ 1 and any p.

Example 8.21

Show that 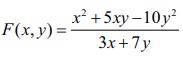 is a homogeneous function of degree 1.

Solution

We compute

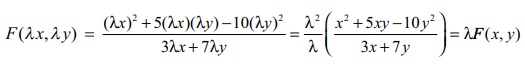
for all λ ∈ ℝ. So F is a homogeneous function of degree 1.

We state the following theorem of Leonard Euler on homogeneous functions.

Definition 8.13 (Euler)

Suppose that A = {( x, y ) | a < b, c < y < d }⊂ ℝ², F : A → ℝ² . If F is having continuous partial derivatives and homogeneous on A , with degree p , then

Suppose that B = {( x, y , z) | a < x < b, c < y < d, u < z < v} ⊂ ℝ³ , F : B → ℝ³. If F is having continuous partial derivatives and homogeneous on B , with degree p , then

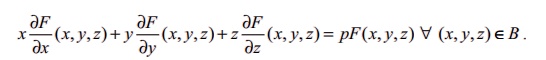
We omit the proof. The above theorem is also true for any homogeneous function of n variables; and is useful in certain calculations involving first order partial derivatives.

Example 8.22

Solution

Note that the function u is not homogeneous. So we cannot apply Euler’s Theorem for u.

However, note that  is homogeneous; because

Note:

Solving this problem by direct calculation will be possible; but will involve lengthy calculations.