Chapter: Artificial Intelligence
Breadth First Search (BFS): Concept, Implementation, Advantages, Disadvantages
Breadth First Search (BFS)
Breadth first search is a general technique of traversing a graph. Breadth first search may use more memory but will always find the shortest path first. In this type of search the state space is represented in form of a tree. The solution is obtained by traversing through the tree. The nodes of the tree represent the start value or starting state, various intermediate states and the final state. In this search a queue data structure is used and it is level by level traversal. Breadth first search expands nodes in order of their distance from the root. It is a path finding algorithm that is capable of always finding the solution if one exists. The solution which is found is always the optional solution. This task is completed in a very memory intensive manner. Each node in the search tree is expanded in a breadth wise at each level.
Concept:
Step 1: Traverse the root node
Step 2: Traverse all neighbours of root node.
Step 3: Traverse all neighbours of neighbours of the root node.
Step 4: This process will continue until we are getting the goal node.
Algorithm:
Step 1: Place the root node inside the queue.
Step 2: If the queue is empty then stops and return failure.
Step 3: If the FRONT node of the queue is a goal node then stop and return success.
Step 4: Remove the FRONT node from the queue. Process it and find all its neighbours that are in ready state then place them inside the queue in any order.
Step 5: Go to Step 3.
Step 6: Exit.
Implementation:
Let us implement the above algorithm of BFS by taking the following suitable example.
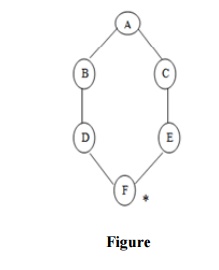
Consider the graph in which let us take A as the starting node and F as the goal node (*)
Step 1:
Place the root node inside the queue i.e. A
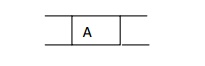
Step 2:
Now the queue is not empty and also the FRONT node i.e. A is not our goal node. So move to step 3.
Step 3:
So remove the FRONT node from the queue i.e. A and find the neighbour of A i.e. B and C
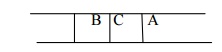
Step 4:
Now b is the FRONT node of the queue .So process B and finds the neighbours of B i.e. D.
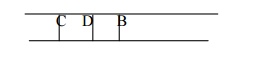
Step 5:
Now find out the neighbours of C i.e. E

Advantages:
In this procedure at any way it will find the goal.
It does not follow a single unfruitful path for a long time. It finds the minimal solution in case of multiple paths.
Disadvantages:
BFS consumes large memory space. Its time complexity is more.
It has long pathways, when all paths to a destination are on approximately the same search depth.
Related Topics