Miller Indices

Miller Indices

The geometry of a crystal may be completely defined with the help of coordinate axes all meeting at a point (origin). The number and inclination of these crystal intercept them at definite distances from the origin or are parallel to some of the axes, i.e., intercepting at infinity. The law of rational indices or intercepts states that it is possible to choose along the three coordinate axes unit distances (a, b, c) not necessarily of the same length such that the ratio of the intercepts of any plane in the crystal is given by (la : mb : nc) where l, m and n are simple integers like 1, 2, 3 or fractions of whole numbers.

For example consider plane LMN in the crystal shown in Fig.

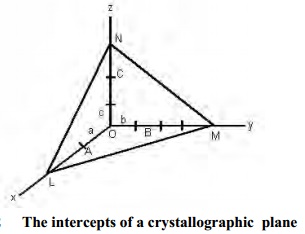
This plane has intercepts OL, OM and ON along the x-, y- and z-axes at distances 2a, 4b and 3c respectively, when OA = a, OB = b and OC = c are the chosen unit distances along the three coordinates. These intercepts are in the ratio of 2a : 4b : 3c wherein 2, 4, 3 are simple integral whole numbers.

The coefficients of a, b and c (2, 4 and 3 in this case) are known as the Weiss indices of a plane. It may be borne in mind that the Weiss indices are not always simple integral whole numbers as in this case. They may have fractional values as well as infinity (an indefinite quantity). Weiss indices are, therefore, rather awkward in use and have consequently been replaced by miller indices. Taking the reciprocals of Weiss indices and multiplying throughout by the smallest number in order to make all reciprocals as integers obtain the Miller indices of a plane. The Miller indices for a particular family of planes are usually written (h, k, l) where h, k and l are positive or negative integers or zero.

Consider a plane which in Weiss notation is given by 2 a: 4b: 3c. Taking reciprocals of coefficients of a, b and c, we get the ratio 1/2, 1/4, 1/3. Multiplying by 12 in order to convert them into whole numbers, we get 6, 3, 4. These numbers are called the Miller indices of the plane, and the plane is designated as the (634) plane. In (634) plane, h = 6, k = 3 and l = 4.

Similarly the Miller's indices for the plane which the Weiss notation is given by ¥ a : 2b : c. Taking reciprocals of coefficients of a, b and c, we get the ratio 1/¥, 1/2, 1/1, i.e., 0, 1/2, 1. Multiplying by 2 in order to convert them into whole numbers, we get 0, 1, 2. The plane is designated as the (012) plane in which , h = 0, k = 1 and l = 2.

The distances between parallel planes in a crystal are designated as d_hkl. For different cubic lattices these interplanar spacings are given by the general formula

d_hkl = a / root of(h² + k² + l²)

Where a is the length of the cube side while h, k and l are the Miller indices of the plane.

Definition of Miller Indices in three dimensions

A pair of planes with Miller indices (213)

The Miller indices of a face of a crystal are inversely proportional to the intercepts of that face on the various axes.

The Miller indices of this particular family of planes are given by the reciprocals of the fractional intercepts along each of the cell directions. E.g. 1/2 x a, 1x b, 1/3 x c.

The procedure for determining the miller indices for a plane is as follows:

1.     Prepare a three-column table with the unit cell axes at the tops of the columns.

2.     Enter in each column the intercept (expressed as a multiple of a, b or c) of the plane with these axes.

3.     Invert all numbers.

4.     Clear fractions to obtain h, k and l.

Consider the x-, y-, z- axes in the above figure with the dots representing atoms in a single crystal lattice. To determine the Miller indices, one finds the intercepts on the three axis. The intercepts are: x = 4, y = 2 and z = 3. Then the reciprocals are taken, ie., ¼, ½, 1/3 and finally these fractions are reduced to the smallest integers, ie., 3, 6, 4 by 12. These are the Miller indices represented as (364).

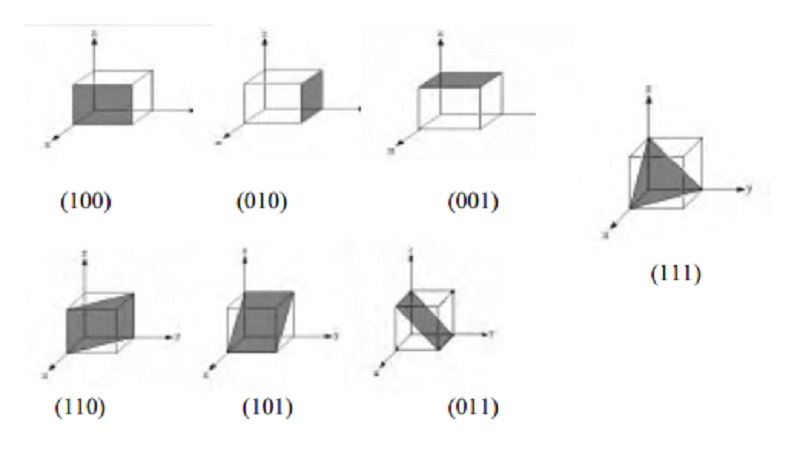
Let us look at the most common planes in a cube, shown below in figure. As an example the front crystal face shown here intersects the x-axis but does not intersect the y- or z -axes but parallel to y and z axis. The front crystal face intersects only one of the crystallographic axes(x-axes). So the miller indices for the plane is (100). The side plane has intercepts

x = ¥, y = 1, z = ¥ because the plane is parallel to the x- and z-axes, forming the Miller indices gives (010). The top plane has intercepts x = ¥, y = ¥ , z = 1 because the plane is parallel to the x- and y- axes , forming the Miller indices gives (001).

The (110) plane intercepts x=1, y=1 and z= ¥ which is parallel to z-axis. Similarly the other two planes are (101) and (011). The (111) plane intercepts all the three axes x=1, y=1 and z=1.