Van't Hoff Equation

Van't Hoff Equation

This equation gives the quantitative temperature dependence of equilibrium constant (K). The relation between standard free energy change (ΔG°) and equilibrium constant is

Differentiating equation (3) with respect to temperature,

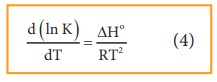
Equation 4 is known as differential form of van’t Hoff equation.

On integrating the equation 4, between T₁ and T₂ with their respective equilibrium constants K₁ and K₂.

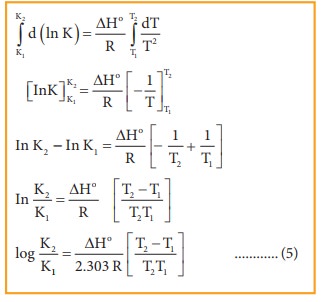
Equation 5 is known as integrated form of van’t Hoff equation. 

Problem

For an equilibrium reaction K_p = 0.0260 at 25° C ΔH= 32.4 kJmol^-1, calculate K_p at 37° C

Solution:

T₁=25 + 273 = 298 K

T₂ = 37 + 273 = 310 K

ΔH = 32.4 KJmol^-1 = 32400 Jmol^-1

R=8.314 JK^-1 mol^-1

K_P1= 0.0260

K_p2=?