Brief questions and answers: Physical and Chemical Equilibrium

Physical and Chemical Equilibrium | Chemistry

Answer the following questions

26. If there is no change in concentration, why is the equilibrium state considered dynamic ?

● The equilibrium constant does not indicate whether a reaction is in static or dynamic equilibrium.

● It is simply the concentrations of products divided by the concentrations of reactants.

● A reaction is dynamic equilibrium if the rate of the forward reaction is equal to the rate of backward reaction.

27. For a given reaction at a particular temperature, the equilibrium constant has constant value. Is the value of Q also constant ? Explain.

Q is a reaction quotient, which helps to determine if a reaction will shift forward or backward direction. As a system approaches towards equilibrium, Q approaches towards K. 

28. What the relation between KP and KC. Give one example for which KP is equal to KC.

The relation between equilibrium constants K_P and K_c are given by

 K_P= Kc (RT)^Δn_g

 Δ_ng = 2 – 2 = 0

H_2(g) + I_2(g) → 2HI_(g)

K_P = K_C

29. For a gaseous homogeneous reaction at equilibrium, number of moles of products are greater than the number of moles of reactants. Is KC is larger or smaller than KP.

For a gaseous homogenious equilibrium reaction at equilibrium, number of moles of products are greater than the number of moles of reactants.

For example PCl_5(g) ⇌ PCl_3(g) + Cl_2(g)

Δ_ng = 2 − 1 = 1 positive

The relation between K_P & K_C for above reaction is K_P > K_C. Hence K_C is smaller than K_P.

30. When the numerical value of the reaction quotient (Q) is greater than the equilibrium constant (K), in which direction does the reaction proceed to reach equilibrium ?

When the numerical value of reaction quotient Q is greater then the equilibrium constant K_C. Q > K_C. The equilibrium shift to the left and produce more reactants.

31. For the reaction,

A2(g) + B2(g) ⇌ 2AB(g) ; ΔH is –ve.

the following molecular scenes represent different reaction mixture (A – green, B – blue)

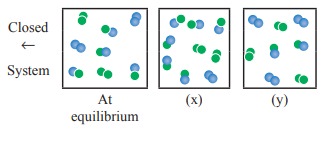
i) Calculate the equilibrium constant KP and (KC).

ii) For the reaction mixture represented  by scene (x), (y) the reaction proceed  in which directions ?

iii) What is the effect of increase in pressure  for the mixture at equilibrium.

Solution:

i) K_C= [AB]² / [A₂] [B₂]

A – Green

 B – blue

Given that 'V' is constant (closed system)

At equilibrium

∴K_C = [ (4/V)² ] / [ (2/V) (2/V) ] = 16 / 4 = 4

K_P = K_C (RT)^Δng

K_P = 4 (RT)^o = 4

ii) At Stage 'x'

Q = ( [AB]² ) / ( [A₂] [B₂] ) = (6/V)²  / ( (2/V) (1/V) ) = 36/2 = 18

Q > K_C ie., reverse reaction is favoured

iii) At stage 'y'

Q = (3/V)² / ( (3/V)(3/V) ) = 9 / (3× 3) = 1

K_C > Q ie., forward reaction is favoured.

32. State Le-Chatelier principle.

If a system at equilibrium is disturbed, then the equilibrium shifts itselft in a direction that nullifies the effect of that disturbance.

33. Consider the following reactions,

a) H2(g) + I2(g) ⇌ 2 HI

b) CaCO3 (s) ⇌ CaO (s) + CO2(g)

c) S(s) + 3F2 (g) ⇌ SF6 (g)

In each of the above reaction find out whether you have to increase (or) decrease the volume to increase the yield of the product.

Ans: Δ_ng = 2−2 = 0

a) The number of moles of products is equal to the number of moles of reactants, so change in pressure has no effect on equilibrium.

b) Δn_g = 1− 0 = 1

Δn_g = +ve

(ie) To increase the yield of product pressure should be decrease and hence volume increases

c) Δn_g = 1−3 = −2

Δn_g = -ve

(ie) pncrease in pressure favours formation of product hence volume should be decreased

34. State law of mass action.

At any instant, the rate of chemical reaction at a given temperature is directly proportional to the product of the active mass of the reactants at that instant.

35. Explain how will you predict the direction of a equilibrium reaction.

The direction of equilibrium reaction can be predicted by comparing Q with K_C.

● Q = K_C ; the reaction is in equilibrium state.

● Q > K_C ; the reaction will proceed in the reverse direction i.e formation of reactants.

● Q < K_C, the reaction will proceed in the forward direction ie the formation of products.

36. Derive a general expression for the equilibrium constant KP and KC for the reaction

3H2(g) + N2(g) ⇌ 2NH3(g)

Synthesis of ammonia:

Let us consider the formation of ammonia in which 'a' moles nitrogen and 'b' moles hydrogen gas are allowed to react in a container of volume V. Let 'x' moles of nitrogen react with 3x moles of hydrogen to give 2x moles off ammonia.

N_2(g) + 3H_2(g) ⇌ 2NH_3(g)

The equilibrium constant Kp can be also be calculated as follows:

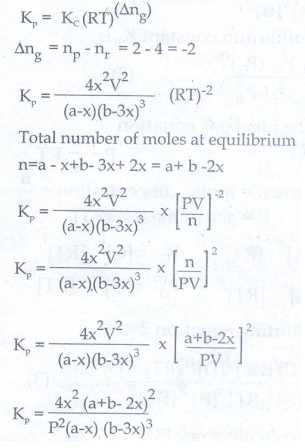
37.  Write a balanced chemical equation for a equilibrium reaction for which the equilibrium constant is given by expression

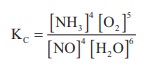
Solution:

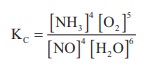
K_C = [NH₃]⁴[O₂]⁵ / [NO]⁴[H₂O]⁶

Chemical equation is

4NO + 6H₂O ⇌ 4NH₃ +5O₂

38. What is the effect of added inert gas on the reaction at equilibrium at constant volume.

When an inert gas is added to an equilibrium system at constant volume, the partial pressures of reactants and the products are unchanged. Hence it has no effect on chemical equilibrium.

39. Derive the relation between KP and KC For general equilibrium reaction.

Let us consider the general equilibrium reaction in which all reactants and products are ideal gases.

xA + y B → lC + mD

The equilibrium constant K_C is

K_C = [C]^l [D]^m / [A]^x[B]^y      …………….(1)

The equilibrium constant K_P is

K_P = [ (P_C)^l.(P_D)^m ] / [ (P_A)^x.(P_B)^y   ]    …………….(2)

From the ideal gas equation

PV = nRT

P = n/V RT

Active mass = molar concentration = n / V

P = active mass × (RT)

P_A^x = [A]^x . [RT] ^x

P_C^l = [C] ^l . [RT] ^l

P_B^y = [B]^y . [RT]^y

P_D^m = [D]^m . [RT]^m

on subsituting equation 2

k_P = { [C]^l.[RT]^l [D]^m.[RT]^m } / { [A]^x.[RT] ^x [B]^y.[RT]^y } ………. (3)

k_P = { [C]^l[D]^m[RT]^l+m } / { [A]^x [B]^y[RT]^x+y }

k_P = { [C]^l[D]^m / [A]^x[B]^y } [RT]^{( l + m) - ( x + y)}        …….(4)

By comparing equation (1) & (4) we get

k_P = K_C (RT) ^(Δng) ΔS   ……….(5)

Where Δn_g, is the difference between the sum of number of moles of gaseous products and the sum of the number of moles of gaseous reactants.

40. One mole of PCl5 is heated in one litre closed container. If 0.6 mole of chlorine is found at equilibrium, calculate the value of equilibrium constant.

Solution:

Given that [PCl₅]_initital = 1 mole / 1 dm³

[Cl₂]_eq = 0.6 mole dm⁻³

PCl₅ → PCl₃ + Cl₂

[PCl₃]_eq = 0.6 mole dm⁻³

[PCl₅]_eq = 0.4 mole dm⁻³

K_C = ( [PC1₃][C1₂] ) / [PCl₅]

= (0.6 × 0.6) / 0.4 = 0.9

K_C = 0.9

41. For the reaction

SrCO3 (s) ⇌ SrO (s) + CO2(g),

the value of equilibrium constant KP = 2.2 × 10–4 at 1002 K. Calculate KC for the reaction.

Solution:

For the reaction,

SrCO₃(s) ⇌ SrO (s) + CO₂(g)

Δng = 1 − 0 = 1

K_P = K_C (RT)

2.2 × 10^-4 = K_C (0.0821) (1002)

K_C = ( 2.2× 10^-4 ) / ( 0.0821× 1002 )

 = 0.0267 × 10^-4

 = 2.67 × 10^-6

42.  To study the decomposition of hydrogen iodide, a student fills an evacuated 3 litre flask with 0.3 mol of HI gas and allows the reaction to proceed at 500 0C. At equilibrium he found the concentration of HI which is equal to 0.05 M. Calculate KC and KP.

Solution:

V = 3L

[HI]_initital = 0.3 / 3 = 0.1M

[HI]_eq = 0.05 M

2HI_(g) ⇌ H_2(g) + I_2(g)

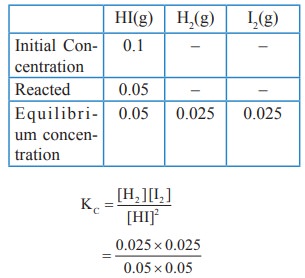
K_C = [H₂] [I₂] / [HI]²

= (0.025 ×0.025) / (0.05)²

K_P = K_C (RT)^Δng

Δng = 2−2 = 0

K_P = 0.25 (RT)°

∴ K_P = 0.25

43. Oxidation of nitrogen monoxide was studied at 200 0C with initial pressures of 1 atm NO and 1 atm of O2. At equilibrium partial pressure of oxygen is found to be 0.52 atm calculate KP value.

Solution:

2NO_(g) + O_2(g) ⇌ 2NO_2(g)

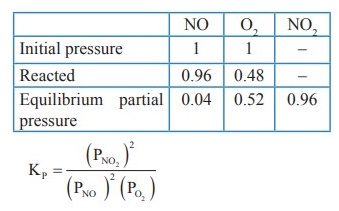
K_P = [P_NO2]²/ ( [P_NO]²[P_O2]) = (0.96 × 0.96) / (0.04 × 0.04 × 0.52)

 = 1.107 × 10³ (atm)⁻¹

44. 1 mol of CH4, 1 mole of CS2 and 2 mol of H2S are 2 mol of H2 are mixed in a 500 ml flask. The equilibrium constant for the reaction KC = 4 × 10–2 mol2 lit–2. In which direction will the reaction proceed to reach equilibrium ?

Solution:

CH_4(g) + 2H₂S_(g) ⇌ CS_2(g) + 4H_2(g)

K_C = 4 ×10⁻² mol²lit⁻²

V = 500 ml = 1/2 L

[CH₄]_in = 1 mol / (½)L = 2 mol L⁻¹ ;

[CS₂]_in = 1 mol / (½)L = 2 mol L⁻¹

[H₂S]_in = 2 mol / (½)L = 4 mol L⁻¹

[H₂]_in = 2 mol / (½)L = 4 mol L⁻¹

Q = ( [CS₂] [H₂]⁴ ) / ( [CH₄] [H₂S]² ) = [ 2 × (4)⁴ ] / [ 2 × (4)² ] = 16

Q > K_C

∴ The reaction will proceed in the reverse direction to reach the equilibrium.

45. At particular temperature KC = 4 × 10–2 for the reaction

H2S(g) ⇌ H2(g) + ½ S2(g)

Calculate KC for each of the following reaction

i) 2H2S (g) ⇌ 2H2 (g) + S2 (g)

ii) 3H2S (g) ⇌ 3H2 (g) + 3/2 S2(g)

Solution:

i) 2H₂S_(g) ⇌ 2H_2(g) + S_2(g)

ii) 3H₂S_(g) ⇌ 3H_2(g) + 3/2 S_2(g)

K_C = 4 × 10⁻² for the reaction,

H₂S_(g) ⇌ H_2(g) + ½ S_2(g).

K_C = ( [H₂] [S₂]^½ ) / [H₂S]

⇒ 4 × 10⁻² = [H₂][S₂] ^½ / [H₂S]

For the reaction,

2H₂S_(g) ⇌ 2H_2(g) + S_2(g)

K_C = ([H₂]²[S₂]) / [H₂S]² = (4 × 10⁻²)²

= 16 × 10^-4

For the reaction,

3H₂S_(g) ⇌ 3H_2(g) + 3/2 S_2(g)

K_C = ([H₂]³[S₂] ^3/2) / [H₂S]³ = (4 × 10⁻²)³

= 64 × 10^-6

46. 28 g of Nitrogen and 6 g of hydrogen were mixed in a 1 litre closed container. At equilibrium 17g NH3 was produced. Calculate the weight of nitrogen, hydrogen at equilibrium.

Solution:

Given,

m_N2 = 28g; m_H2 = 6g;

m_NH3 = 17g ; V = 1 L

(n_N2)_initiaI = 28 / 28 = 1 mol

(n_H2)_initial = 6 / 2 = 3 mol

N_2(g) + 3H_2(g) ⇌ 2NH_3(g)

[NH₃] = (17 / 17 ) = l mol

Weight of N₂ = (no.of moles of N₂) × molar mass of N₂

= 0.5 × 28 =14g

Weight of H₂ = (no.of moles of H₂) × molar mass of H₂

= 1.5 × 2 = 3g

47. The equilibrium for the dissociation of XY2 is given as,

2XY2 (g) ⇌ 2XY (g) + Y2(g)

if the degree of dissociation x is so small compared to one. Show that 2 KP = PX3 where P is the total pressure and KP is the dissociation equilibrium constant of XY2.

Solution:

48. A sealed container was filled with 1 mol of A2 (g), 1 mol B2 (g) at 800 K and total pressure 1.00 bar. Calculate the amounts of the components in the mixture at equilibrium given that K = 1 for the reaction

A2 (g) + B2 (g) ⇌ 2AB (g)

Solution:

49. Deduce the Vant Hoff equation.

50. The equilibrium constant KP for the reaction

N2(g) + 3H2(g) ⇌ 2NH3(g) is 8.19 × 102 at 298 K and 4.6 × 10–1 at 498 K. Calculate ΔH0 for the reaction.

Solution:

 51. The partial pressure of carbon dioxide in the reaction CaCO3 (s) ⇌ CaO (s) + CO2(g) is 1.017 × 10–3 atm at 5000 C. Calculate KP at 6000c C for the reaction. ΔH for the reaction is 181 KJ mol–1 and does not change in the given range of temperature.

Solution:

PCO2 = 1.017x10-3 atm T = 500º C

Kp = PCO2

KP1 = 1.017x10-3  T=500+273=773K

KP2 = ?  T=600+273=873K

∆Hº = 181KJmol-1