Law of mass action

Law of mass action

In 1864 two Norwegian chemists namely Maximilian Guldberg and Peter Waage formulated the law of mass action, based on the experimental studies of many reversible reactions. The law states that,

“At any instant, the rate of a chemical reaction at a given temperature is directly proportional to the product of the active masses of the reactants at that instant”.

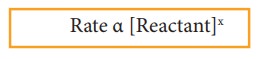
Rate α [Reactant]^x

where, x is the stoichiometric coefficient of the reactant and the square bracket represents the active mass (concentration) of the reactants.

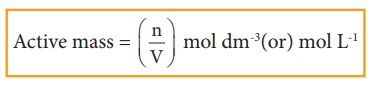
where n is the number of moles and V is the volume of the container (dm³ or L)

Equilibrium constants (K_p and K_C):

Let us consider a reversible reaction,

xA+yB ⇌ lC + mD

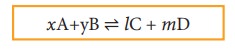
where, A and B are the reactants, C and D are the products and x,y, l and m are the stoichiometric coefficients of A, B, C and D, respectively.

Applying the law of mass action, the rate of the forward reaction,

r_f α [A]^x [B]^y (or) r_f = k_f [A]^x [B]^y

Similarly, the rate of the backward reaction,

r_b α [C]^l [D]^m

(or)

r_b = k_b [C]^l[D]^m

where k_f and k_b are proportionality constants

At equilibrium,

Rate of forward reaction (r_f) = Rate of backward reaction (r_b)

k_f [A]x [B]^y = k_b [C]l [D]^m

where, K_c is the equilibrium constant in terms of concentration (active mass).

At a given temperature, the ratio of the product of active masses of reaction products raised to the respective stoichiometric coefficients in the balanced chemical equation to that of the reactants is a constant, known as equilibrium constant. Later when we study chemical kinetics we will learn that this is only approximately true.

If the reactants and products of the above reaction are in gas phase, then the equilibrium constant can be written in terms of partial pressures as indicated below,

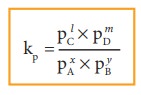
Where, p_A, p_B, p_C,and p_D are the partial pressures of the gas A, B, C and D, respectively.

Relation between K_p and K_c

Let us consider the general reaction in which all reactants and products are ideal gases.

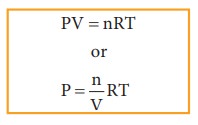
The ideal gas equation is

Since

Active mass = molar concentration = n/V

P = active mass × RT

Based on the above expression the partial pressure of the reactants and products can be expressed as,

p_Ax = [A]^x [RT]^x

p_By = [B]^y [RT]^y

p_C1 = [C]^l [RT]^l

p^m_D = [D]^m [RT]^m

On substitution in Eqn. 2,

By comparing equation (1) and (4), we get

where,

Δn_g is the difference between the sum of number of moles of products and the sum of number of moles of reactants in the gas phase.

The following relations become immediately obvious.

When Δn_g = 0

K_p = K_c (RT)⁰ = K_c

Example:

H₂(g) + I₂(g) ⇌ 2HI (g)

N₂ (g) +O₂ (g) ⇌ 2NO(g)

When Δn_g = +ve

K_p = K_c (RT)^+ve

K_p>K_c

2NH₃(g) ⇌ N₂ (g) + 3H₂ (g)

PCI₅ (g) ⇌ PCl₃ (g) + Cl₂ (g)

When Δn_g = -ve

K_p = K_c (RT)^-ve

K_p< K_c

Example:

2H₂(g) + O₂(g) ⇌ 2H₂O (g)

2SO₂(g) + O₂(g) ⇌ 2SO₃ (g)

Table 8.1 Relation between equilibrium constants for some reversible reactions

Equilibrium constants for heterogeneous equilibrium

Consider the following heterogeneous equilibrium.

CaCO₃ (s) ⇌ CaO (s) + CO₂ (g)

The equilibrium constant for the above reaction can be written as

K_c = [CaO(s)][CO₂(g)] /  CaCO₃ (s)

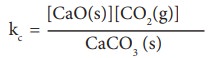
A pure solid always has the same concentration at a given temperature, as it does not expand to fill its container. i.e. it has same number of moles L^-1 of its volume. Therefore, the concentration of a pure solid is a constant. The above expression can be modified as follows

K_c  = [CO₂ (g)]

Or

K_p = p_CO2

The equilibrium constant for the above reaction depends only the concentration of carbon dioxide and not the calcium carbonate or calcium oxide. Similarly, the active mass (concentration) of the pure liquid does not change at a given temperature. Consequently, the concentration terms of pure liquids can also be excluded from the expression of the equilibrium constant.

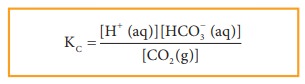
For example,

CO₂(g) + H₂O (l) ⇌ H+(aq) + HCO₃^– (aq)

Since, H₂O (l) is a pure liquid the Kc can be expressed as

Example

Write the K_p and K_c for the following reactions