Types of Matrices

Types of Matrices

Row, Column, Zero matrices

Definition 7.2

A matrix having only one row is called a row matrix.

For instance, A = [A]1×4 = [1 0 − 1.1 √2] is a row matrix. More generally, A = [ aij ]1× n = [a1 j ]1×n is a row matrix of order 1× n .

Definition 7.3

A matrix having only one column is called a column matrix.

For instance, [A]4x1 = 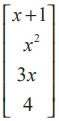is a column matrix whose entries are real valued functions of real variable x. More generally, A = [ aij ]m×1 = [ai1 ]m×1  is a column matrix of order m ×1.

Definition 7.4

A matrix A = [aij ]m×n  is said to be a zero matrix or null matrix or void matrix denoted by O if aij  = 0 for all values of 1 ≤ i ≤ m and 1 ≤ j ≤ n.

For instance, [0], 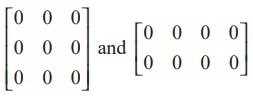are zero matrices of order 1× 1, 3× 3 and 2× 4 respectively.

A matrix A is said to be a non-zero matrix if at least one of the entries of A is non-zero.

Square, Diagonal, Unit, Triangular matrices

Definition 7.5

A matrix in which number of rows is equal to the number of columns, is called a square matrix. That is, a matrix of order n × n is often referred to as a square matrix of order n.

For instance, A = 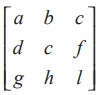is a square matrix of order 3.

Definition 7.6

In a square matrix A = [aij ]n×n of order n, the elements a11 , a22 , a33 ,..., ann are called the principal diagonal or simply the diagonal or main diagonal or leading diagonal elements.

Definition 7.7

A square matrix A = [aij ]n×n  is called a diagonal matrix if aij = 0 whenever i≠j.

Thus, in a diagonal matrix all the entries except the entries along the main diagonal are zero. For instance,

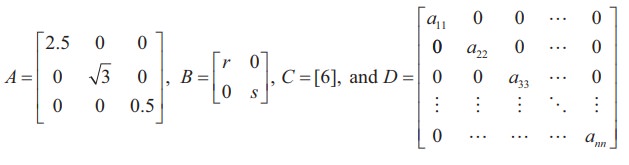
are diagonal matrices of order 3, 2, 1, and n respectively.

Is a square zero matrix, a diagonal matrix?

Definition 7.8

A diagonal matrix whose entries along the principal diagonal are equal is called a Scalar matrix.

That is, a square matrix A = [aij]nxn is said to be a scalar matrix if aij=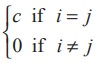

where c is a fixed number. For instance,

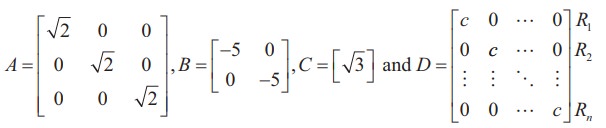
are scalar matrices of order 3, 2, 1, and n respectively.

Observe that any square zero matrix can be considered as a scalar matrix with scalar 0.

Definition 7.9

A square matrix in which all the diagonal entries are 1 and the rest are all zero is called a unit matrix. Thus, a square matrix A = [aij ]n×n  is said to be a unit matrix if

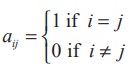
We represent the unit matrix of order n as In .  For instance,

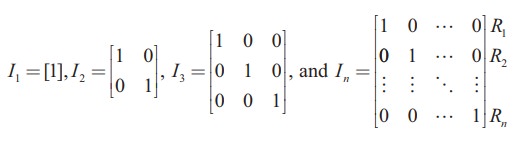
are unit matrices of order 1, 2, 3 and n respectively.

Note 7.1

Unit matrix is an example of a scalar matrix.

There are two kinds of triangular matrices namely upper triangular and lower triangular matrices.

Definition 7.10

A square matrix is said to be an upper triangular matrix if all the elements below the main diagonal are zero.

Thus, the square matrix A = [aij ]n×n is said to be an upper triangular matrix if aij = 0 for all i > j. For instance,

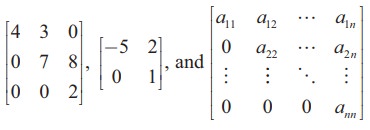
are all upper triangular matrices.

Definition 7.11

A square matrix is said to be a lower triangular matrix if all the elements above the main diagonal are zero.

More precisely, a square matrix A = [aij ]n×n is said to be a lower triangular matrix if aij = 0 for all i < j. For instance,

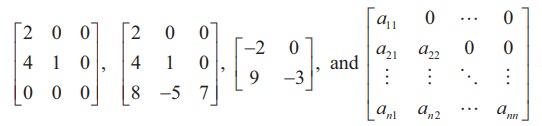
are all lower triangular matrices.

Definition 7.12

A square matrix which is either upper triangular or lower triangular is called a triangular matrix.

Observe that a square matrix that is both upper and lower triangular simultaneously will turn out to be a diagonal matrix.