Definition, Theorem, Solved Example Problems - Application of Factor Theorem to Determinants | 11th Mathematics : UNIT 7 : Matrices and Determinants
Chapter: 11th Mathematics : UNIT 7 : Matrices and Determinants
Application of Factor Theorem to Determinants
Application of Factor Theorem to Determinants.
Theorem 7.3 (Factor Theorem)
If each element of a matrix A is a polynomial in x and if | A | vanishes for x = a, then (x - a) is a factor of | A |.
Note 7.10
(i) This theorem is very much useful when we have to obtain the value of the determinant in ‘factors’ form.
(ii) If we substitute b for a in the determinant | A |, any two of its rows or columns become identical, then | A | = 0, and hence by factor theorem (a - b) is a factor of | A |.
(iii) If r rows (columns) are identical in a determinant of order n (n ≥ r), when we put x = a, then (x - a)r - 1 is a factor of | A |.
(iv) A square matrix (or its determinant) is said to be in cyclic symmetric form if each row is obtained from the first row by changing the variables cyclically.
(v) If the determinant is in cyclic symmetric form and if m is the difference between the degree of the product of the factors (obtained by substitution) and the degree of the product of the leading diagonal elements and if
(1) m is zero, then the required factor is a constant k
(2) m is 1, then the required factor is k(a + b + c) and
(3) m is 2, then the required factor is k(a2 + b2 + c2) + l (ab + bc + ca).


The given determinant is in cyclic symmetric form in x, y and z. Therefore (y - z) and (z - x) are also factors.
The degree of the product of the factors (x − y )( y − z )(z − x) is 3 and the degree of the product of the leading diagonal elements 1× y 2 × z3 is 5.
Therefore the other factor is k (x 2 + y 2 + z 2 ) + (xy + yz + zx) .

Since | A | is in cyclic symmetric form in p, q, r and hence q and r also factors.
Putting p + q + r = 0 ⇒ q + r = - p ; r + p = - q ; and p + q = - r.


That is, by putting sin A = sin B we see that, the given equation is satisfied.
Similarly by putting sin B = sin C and sin C = sin A, the given equation is satisfied.
Thus, we have A = B or B = C or C = A.
In all cases atleast two angles are equal. Thus the triangle is isosceles.
EXERCISE 7.3
Solve the following problems by using Factor Theorem :
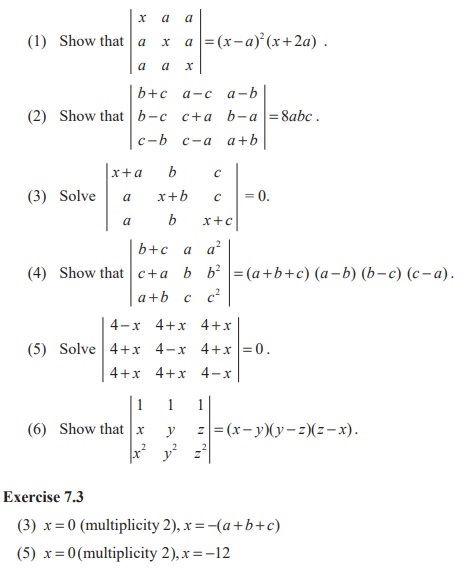
Related Topics