Operation of Transpose of a Matrix and its Properties

Operation of Transpose of a Matrix and its Properties

Definition 7.16

The transpose of a matrix is obtained by interchanging rows and columns of A and is denoted by AT.

More precisely, if A = [aij ]m×n , then AT  = [bij ]n×m , where bij  = a ji  so that the (i, j)th entry of AT  is a ji .

For instance,

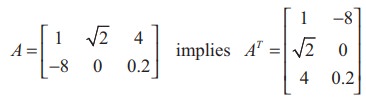
We state a few basic results on transpose whose proofs are straight forward.

For any two matrices A and B of suitable orders, we have

(i) ( AT )T  = A

(ii) (kA)T  = kAT (where k is any scalar)

(iii) ( A + B)T = AT + BT

(iv) ( AB)T =  BT AT (reversal law on transpose)