Definition, General form, Properties, Theorem, Proof, Solved Example Problems, Exercise - Matrices | 11th Mathematics : UNIT 7 : Matrices and Determinants
Chapter: 11th Mathematics : UNIT 7 : Matrices and Determinants
Matrices
Matrices
A matrix is a rectangular array or arrangement of entries or elements displayed in rows and columns put within a square bracket [ ].
In general, the entries of a matrix may be real or complex numbers or functions of one variable (such as polynomials, trigonometric functions or a combination of them) or more variables or any other object. Usually, matrices are denoted by capital letters A, B, C, ... etc. In this chapter the entries of matrices are restricted to either real numbers or real valued functions on real variables.
General form of a matrix
If a matrix A has m rows and n columns, then it is written as
A = [ aij ]m×n ,1 ≤ i ≤ m,1 ≤ j ≤ n.
That is,
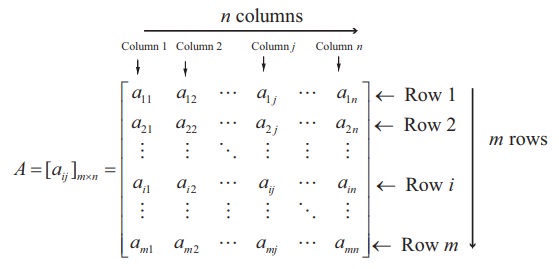
Note that m and n are positive integers.
The following are some examples of matrices :
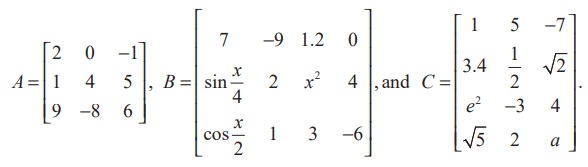
In a matrix, the horizontal lines of elements are known as rows and the vertical lines of elements are known as columns. Thus A has 3 rows and 3 columns, B has 3 rows and 4 columns, and C has 4 rows and 3 columns.
Definition 7.1
If a matrix A has m rows and n columns then the order or size of the matrix A is defined to be m × n (read as m by n).
The objects a11 , a12 , ..., amn are called elements or entries of the matrix A = [aij ]m×n . The element aij is common to ith row and jth column and is called (i, j)th element of A. Observe that the ith row and jth column of A are 1× n and m ×1 matrices respectively and are given by [ai1 a i2 ... a in ] and 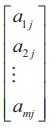
We shall now visualize the representation and construction of matrices for simplifying day-to-day problems.
Illustration 7.1
Consider the marks scored by a student in different subjects and in different terminal examinations. They are exhibited in a tabular form as given below :

This tabulation represents the above information in the form of matrix. What does the entry in the third row and second column represent?
The above information may be represented in the form of a 3 × 5 matrix A as

The entry 84 common to the third row and the second column in the matrix represents the mark scored by the student in English Exam 3.
Example 7.1
Suppose that a matrix has 12 elements. What are the possible orders it can have? What if it has 7 elements?
Solution
The number of elements is the product of number of rows and number of columns. Therefore, we will find all ordered pairs of natural numbers whose product is 12. Thus, all the possible orders of the matrix are 1× 12, 12× 1, 2× 6, 6× 2, 3× 4 and 4× 3.
Since 7 is prime, the only possible orders of the matrix are 1 × 7 and 7 × 1.
Example 7.2
Construct a 2 × 3 matrix whose (i, j)th element is given by
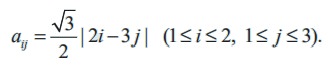
Solution
In general, a 2 × 3 matrix is given by
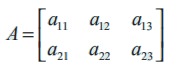
By definition of aij, we easily have a11 = 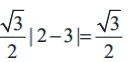 and other entries of the matrix
and other entries of the matrix
A may be computed similarly. Thus, the required matrix A is
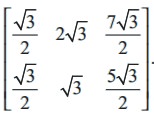
Types of Matrices
Row, Column, Zero matrices
Definition 7.2
A matrix having only one row is called a row matrix.
For instance, A = [A]1×4 = [1 0 − 1.1 √2] is a row matrix. More generally, A = [ aij ]1× n = [a1 j ]1×n is a row matrix of order 1× n .
Definition 7.3
A matrix having only one column is called a column matrix.
For instance, [A]4x1 = 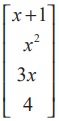 is a column matrix whose entries are real valued functions of real variable x. More generally, A = [ aij ]m×1 = [ai1 ]m×1 is a column matrix of order m ×1.
is a column matrix whose entries are real valued functions of real variable x. More generally, A = [ aij ]m×1 = [ai1 ]m×1 is a column matrix of order m ×1.
Definition 7.4
A matrix A = [aij ]m×n is said to be a zero matrix or null matrix or void matrix denoted by O if aij = 0 for all values of 1 ≤ i ≤ m and 1 ≤ j ≤ n.
For instance, [0], 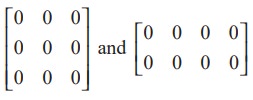 are zero matrices of order 1× 1, 3× 3 and 2× 4 respectively.
are zero matrices of order 1× 1, 3× 3 and 2× 4 respectively.
A matrix A is said to be a non-zero matrix if at least one of the entries of A is non-zero.
Square, Diagonal, Unit, Triangular matrices
Definition 7.5
A matrix in which number of rows is equal to the number of columns, is called a square matrix. That is, a matrix of order n × n is often referred to as a square matrix of order n.
For instance, A = 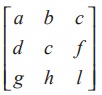 is a square matrix of order 3.
is a square matrix of order 3.
Definition 7.6
In a square matrix A = [aij ]n×n of order n, the elements a11 , a22 , a33 ,..., ann are called the principal diagonal or simply the diagonal or main diagonal or leading diagonal elements.
Definition 7.7
A square matrix A = [aij ]n×n is called a diagonal matrix if aij = 0 whenever i≠j.
Thus, in a diagonal matrix all the entries except the entries along the main diagonal are zero. For instance,
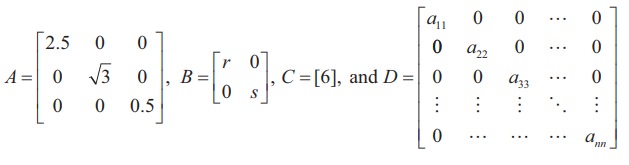
are diagonal matrices of order 3, 2, 1, and n respectively.
Is a square zero matrix, a diagonal matrix?
Definition 7.8
A diagonal matrix whose entries along the principal diagonal are equal is called a Scalar matrix.
That is, a square matrix A = [aij]nxn is said to be a scalar matrix if aij= 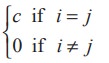
where c is a fixed number. For instance,
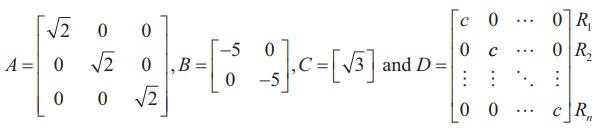
are scalar matrices of order 3, 2, 1, and n respectively.
Observe that any square zero matrix can be considered as a scalar matrix with scalar 0.
Definition 7.9
A square matrix in which all the diagonal entries are 1 and the rest are all zero is called a unit matrix. Thus, a square matrix A = [aij ]n×n is said to be a unit matrix if
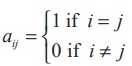
We represent the unit matrix of order n as In . For instance,
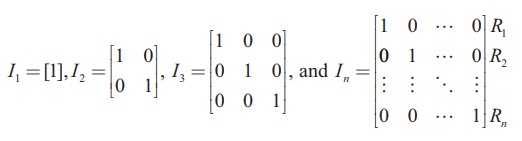
are unit matrices of order 1, 2, 3 and n respectively.
Note 7.1
Unit matrix is an example of a scalar matrix.
There are two kinds of triangular matrices namely upper triangular and lower triangular matrices.
Definition 7.10
A square matrix is said to be an upper triangular matrix if all the elements below the main diagonal are zero.
Thus, the square matrix A = [aij ]n×n is said to be an upper triangular matrix if aij = 0 for all i > j. For instance,
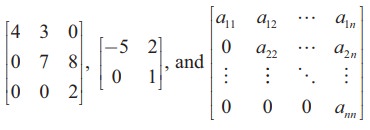
are all upper triangular matrices.
Definition 7.11
A square matrix is said to be a lower triangular matrix if all the elements above the main diagonal are zero.
More precisely, a square matrix A = [aij ]n×n is said to be a lower triangular matrix if aij = 0 for all i < j. For instance,
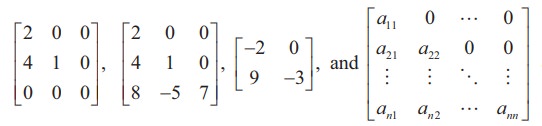
are all lower triangular matrices.
Definition 7.12
A square matrix which is either upper triangular or lower triangular is called a triangular matrix.
Observe that a square matrix that is both upper and lower triangular simultaneously will turn out to be a diagonal matrix.
Equality of Matrices
Definition 7.13
Two matrices A = [ aij ] and B = [bij ] are equal (written as A = B) if and only if
(i) both A and B are of the same order
(ii) the corresponding entries of A and B are equal. That is, aij = bij for all i and j.
For instance, if
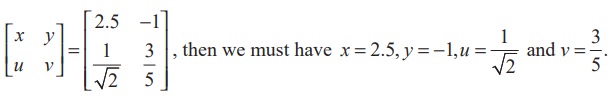
Definition 7.14
Two matrices A and B are called unequal if either of condition (i) or (ii) of Definition 7.13 does not hold.
For instance, 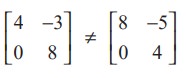 as the corresponding entries are not equal. Also
as the corresponding entries are not equal. Also 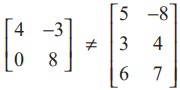 as the orders are not the same.
as the orders are not the same.
Example 7.3
Find x, y, a, and b if
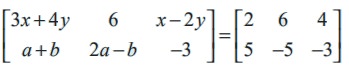
Solution
As the orders of the two matrices are same, they are equal if and only if the corresponding entries are equal. Thus, by comparing the corresponding elements, we get
3x + 4 y = 2, x − 2 y = 4,
a + b = 5,
and 2a − b = −5.
Solving these equations, we get x = 2, y = −1, a = 0, and b = 5.
Algebraic Operations on Matrices
Basic operations on matrices are
(1) multiplication of a matrix by a scalar,
(2) addition/subtraction of two matrices, and
(3) multiplication of two matrices.
There is no concept of dividing a matrix by another matrix and thus, the operation A/B , where A and B are matrices, is not defined.
(1) Multiplication of a matrix by a scalar
For a given matrix A = [aij ]m×n and a scalar k, we define a new matrix kA = [bij ]m×n , where bij = kaij for all i and j.
For instance, if
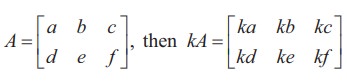
In particular if k = −1 , we obtain − A = [ −aij ]m×n . This - A is called negative of the matrix A.
Don’t say - A as a negative matrix.
(2) Addition and Subtraction of two matrices
If A and B are two matrices of the same order, then their sum denoted by A + B, is again a matrix of same order, obtained by adding the corresponding entries of A and B.
More precisely, if A = [ aij ]m× n and B = [bij ]m×n are two matrices, then the sum A + B of A and B is a matrix given by
A + B = [cij ]m×n where cij = aij + bij for all i and j.
Similarly subtraction A - B is defined as A − B = A + ( −1) B.
That is, A − B = [d ij ]m×n , where d ij = aij − bij ∀ i and j. (The symbol ∀ denotes for every or for all).
Note 7.2
(i) If A and B are not of the same order, then A + B and A - B are not defined.
(ii) The addition and subtraction can be extended to any finite number of matrices.
Example 7.4
Compute A + B and A - B if
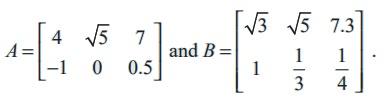
Solution
By the definitions of addition and subtraction of matrices, we have
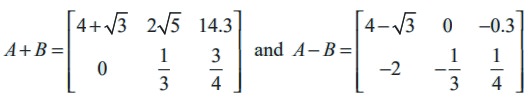
Example 7.5
Find the sum A + B + C if A, B, C are given by
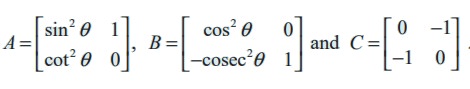
Solution
By the definition of sum of matrices, we have
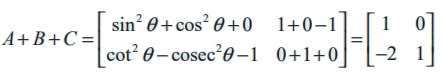
Example 7.6
Determine 3B + 4C - D if B, C, and D are given by
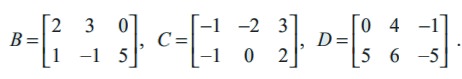
Solution
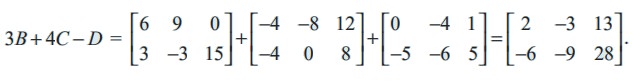
Example 7.7
Simplify :
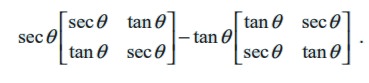
Solution
If we denote the given expression by A, then using the scalar multiplication rule, we get
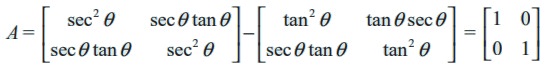
(3) Multiplication of matrices
Definition 7.15
A matrix A is said to be conformable for multiplication with a matrix B if the number of columns of A is equal to the number of rows of B.
That is, if A = [ a ij ]m× n and B = [b ij]n× p are given two matrices, then the product of matrices A and B is denoted by AB and its order is m × p.
The order of AB is m × p = (number of rows of A)× (number of columns of B).

If A = [a1 a2 ... an ]1×n and B =  ,then AB is a matrix of order 1 × 1, that gives a single element which is defined by
,then AB is a matrix of order 1 × 1, that gives a single element which is defined by


where c11 = 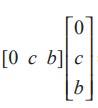 = 0 ⋅ 0 + c ⋅ c + b ⋅ b = c 2 + b2 and other elements cij may be computed similarly.
= 0 ⋅ 0 + c ⋅ c + b ⋅ b = c 2 + b2 and other elements cij may be computed similarly.
Finally, we easily obtain that
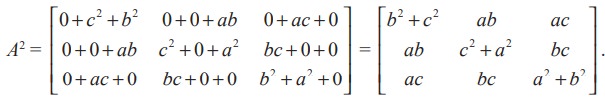

Note 7.3
We have the following important observations:
(1) If A = [aij ]m× n and B = [bij ]n× p , and m ≠ p, then the product AB is defined but not BA.
(2) The fundamental properties of real numbers namely,
ab = ba ∀a ,b ∈R
ab = ac ⇒ b = c ∀ a,b, c ∈R, a ≠ 0
ab = 0 ⇒ a = 0 or b = 0 ∀ a ,b ∈R
Can we discuss these in matrices also?
(i) Even if AB and BA are defined, then AB = BA is not necessarily true.
For instance, we consider
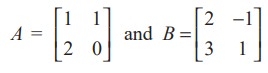
and observe that AB ≠ BA, since
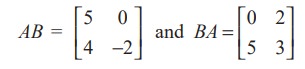
In this case we say that A and B do not commute (with respect to multiplication)
Observe that AB = BA is also possible. For instance,
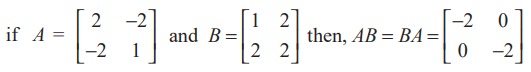
In this case we say that A and B commute with respect to multiplication.
(ii) Cancellation property does not hold for matrix multiplication. That is, A ≠ O, B, and C are three square matrices of same order n × n with n > 1, then AB = AC does not imply B = C and BA = CA does not imply B = C.
As a simple demonstration of these facts, we observe that for instance,
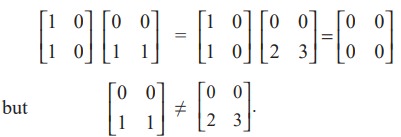
(iii) It is possible that AB = O with A ≠ O and B ≠ O; Equivalently, AB = O is not necessarily imply either A = O or B = O. The following relation demonstrates this fact :
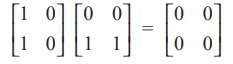
(3) In general, for any two matrices A and B which are conformable for addition and multiplication, for the below operations, we have
(A±B)2 need not be equal to A 2±2 AB B2
A 2-B2 need not be equal to ( A+B)( A-B).
Example 7.10
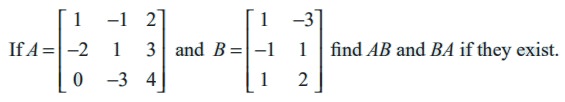
Solution
The order of A is 3 × 3 and the order of B is 3 × 2. Therefore the order of AB is 3 × 2. A and B are conformable for the product AB. Call C = AB. Then,
c11 = (first row of A) (first column of B)
Similarly c12 = 0, c21 = 0, c22 = 13, c31 = 7, c32 = 5.
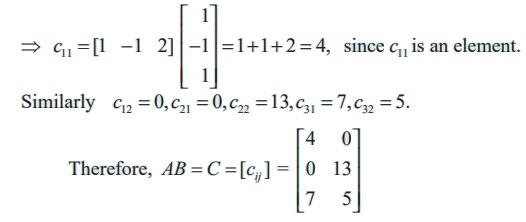
The product BA does not exist, because the number of columns in B is not equal to the number of rows in A.
Example 7.11
A fruit shop keeper prepares 3 different varieties of gift packages. Pack-I contains 6 apples, 3 oranges and 3 pomegranates. Pack-II contains 5 apples, 4 oranges and 4 pomegranates and Pack –III contains 6 apples, 6 oranges and 6 pomegranates. The cost of an apple, an orange and a pomegranate respectively are Rs. 30, Rs. 15 and Rs. 45. What is the cost of preparing each package of fruits?
Solution
Cost matrix A = [30 15 45],

Cost of packages are obtained by computing AB. That is, by multiplying cost of each item in A (cost matrix A) with number of items in B (Fruit matrix B).
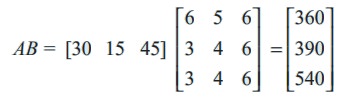
Pack-I cost Rs. 360, Pack-II cost Rs. 390, Pack-III costs Rs. 540.
Properties of Matrix Addition, Scalar Multiplication and Product of Matrices
Let A, B, and C be three matrices of same order which are conformable for addition and a, b be two scalars. Then we have the following:
(1) A + B yields a matrix of the same order
(2) A + B = B + A (Matrix addition is commutative)
(3) (A + B) + C = A + (B + C) (Matrix addition is associative)
(4) A + O = O + A = A (O is additive identity)
(5) A + (- A)=O = (- A) + A (- A is the additive inverse of A)
(6) (a + b)A = aA + bA and a(A + B) = aA + aB
(7) a(bA) =(ab)A, 1A = A and 0A = O.
Properties of matrix multiplication
Using the algebraic properties of matrices we have,
• If A, B, and C are three matrices of orders m × n, n × p and p × q respectively, then A(BC) and (AB)C are matrices of same order m × q and
A(BC) = (AB)C (Matrix multiplication is associative).
•If A, B, and C are three matrices of orders m × n, n × p, and n × p respectively, then A(B + C) and AB + AC are matrices of the same order m × p and
• A(B + C) = AB + AC. (Matrix multiplication is left distributive over addition)
If A, B, and C are three matrices of orders m × n, m × n, and n × p respectively, then (A + B)C and AC + BC are matrices of the same order m × p and
(A + B)C = AC + BC. (Matrix multiplication is right distributive over addition).
• If A, B are two matrices of orders m × n and n × p respectively and α is scalar, then α(AB) = A(α B) = (α A)B is a matrix of order m × p.
If I is the unit matrix, then AI = IA = A (I is called multiplicative identity).
Operation of Transpose of a Matrix and its Properties
Definition 7.16
The transpose of a matrix is obtained by interchanging rows and columns of A and is denoted by AT.
More precisely, if A = [aij ]m×n , then AT = [bij ]n×m , where bij = a ji so that the (i, j)th entry of AT is a ji .
For instance,
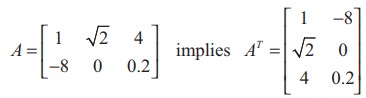
We state a few basic results on transpose whose proofs are straight forward.
For any two matrices A and B of suitable orders, we have
(i) ( AT )T = A
(ii) (kA)T = kAT (where k is any scalar)
(iii) ( A + B)T = AT + BT
(iv) ( AB)T = BT AT (reversal law on transpose)


Symmetric and Skew-symmetric Matrices
Definition 7.17
A square matrix A is said to be symmetric if AT = A.
That is, A = [ aij ]n×n is a symmetric matrix, then aij = a ji for all i and j.
For instance, 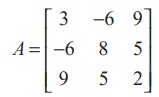 is a symmetric matrix since AT =A.
is a symmetric matrix since AT =A.
Observe that transpose of AT is the matrix A itself. That is ( AT )T=A.
Definition 7.18
A square matrix A is said to be skew-symmetric if AT = − A.
If A = [aij ]n×n is a skew-symmetric matrix, then aij = −a j for all i and j.
Now, if we put i = j, then 2aii = 0 or aii = 0 for all i. This means that all the diagonal elements of a skew-symmetric matrix are zero.
For instance, A =
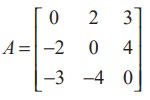
is a skew-symmetric matrix since AT= - A
It is interesting to note that any square matrix can be written as the sum of symmetric and skew-symmetric matrices.
Theorem 7.1
For any square matrix A with real number entries, A + AT is a symmetric matrix and A − AT is a skew-symmetric matrix.
Proof
Let B = A + AT.
BT = ( A + AT )T = AT + ( AT )T = AT + A = A + AT = B .
This implies A + AT is a symmetric matrix.
Next, we let C = A − AT . Then we see that
C T = ( A + ( − AT ))T = AT + ( − AT )T = AT − ( AT )T = AT − A = − ( A − AT ) = − C
This implies A − AT is a skew-symmetric matrix.
Theorem 7.2
Any square matrix can be expressed as the sum of a symmetric matrix and a skew-symmetric matrix.
Proof
Let A be a square matrix. Then, we can write
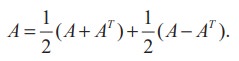
From Theorem 7.1, it follows that (A+AT) and (A-AT) are symmetric and skew-symmetric matrices respectively. Since (kA)T = kAT , it follows that 1/2( A + AT ) and 1/2( A − AT ) are symmetric and skew-symmetric matrices, respectively. Now, the desired result follows.
Note 7.4
A matrix which is both symmetric and skew-symmetric is a zero matrix.
Example 7.13
Express the matrix 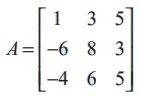 as the sum of a symmetric and a skew-symmetric matrices.
as the sum of a symmetric and a skew-symmetric matrices.
Solution

Thus A is expressed as the sum of symmetric and skew-symmetric matrices.
EXERCISE 7.1
(1) Construct an m × n matrix A = [aij ], where aij is given by

(10) Give your own examples of matrices satisfying the following conditions in each case:
(i) A and B such that AB ≠ BA .
(ii) A and B such that AB = O = BA, A ≠ O and B ≠ O.
(iii) A and B such that AB = O and BA ≠ O.
(11) Show that f(x)f(y)= f(x+y) where
(12) If A is a square matrix such that A2 = A, find the value of 7A - (I + A)3.
(13) Verify the property A(B + C) = AB + AC, when the matrices A, B, and C are given by
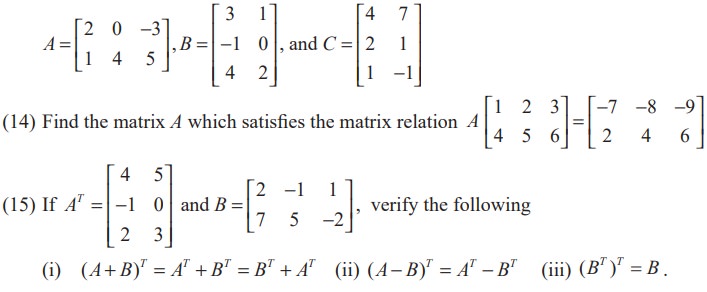
(16) If A is a 3 × 4 matrix and B is a matrix such that both AT B and BAT are defined, what is the order of the matrix B?
(17) Express the following matrices as the sum of a symmetric matrix and a skew-symmetric matrix:
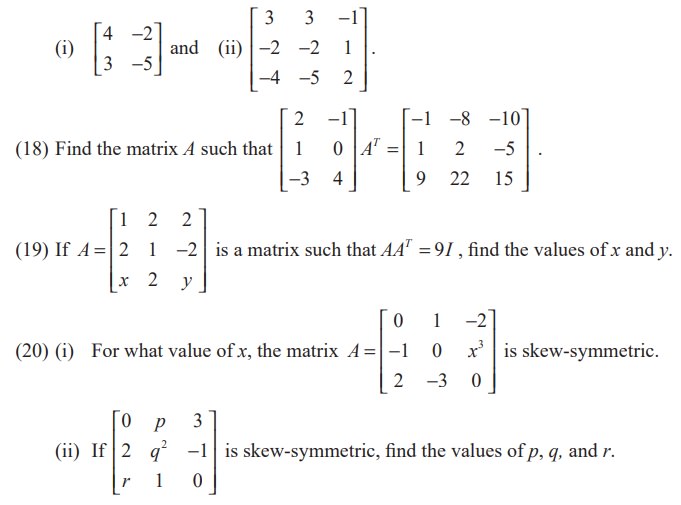
(21) Construct the matrix A = [aij ]3×3 , where aij = i − j . State whether A is symmetric or skew-symmetric.
(22) Let A and B be two symmetric matrices. Prove that AB = BA if and only if AB is a symmetric matrix.
(23) If A and B are symmetric matrices of same order, prove that
(i) AB + BA is a symmetric matrix.
(ii) AB - BA is a skew-symmetric matrix.
(24) A shopkeeper in a Nuts and Spices shop makes gift packs of cashew nuts, raisins and almonds.
Pack I contains 100 gm of cashew nuts, 100 gm of raisins and 50 gm of almonds.
Pack-II contains 200 gm of cashew nuts, 100 gm of raisins and 100 gm of almonds.
Pack-III contains 250 gm of cashew nuts, 250 gm of raisins and 150 gm of almonds.
The cost of 50 gm of cashew nuts is Rs. 50, 50 gm of raisins is Rs. 10, and 50 gm of almonds is Rs. 60. What is the cost of each gift pack?

Related Topics