Equality of Matrices

Equality of Matrices

Definition 7.13

Two matrices A = [ aij ] and B = [bij ] are equal (written as A = B) if and only if

(i) both A and B are of the same order

(ii) the corresponding entries of A and B are equal. That is, aij  = bij  for all i and j.

For instance, if

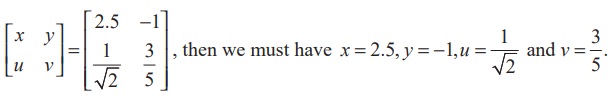
Definition 7.14

Two matrices A and B are called unequal if either of condition (i) or (ii) of Definition 7.13 does not hold.

For instance, 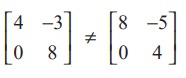as the corresponding entries are not equal. Also   as the orders are not the same.

Example 7.3

Find x, y, a, and b if

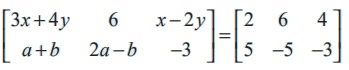
Solution

As the orders of the two matrices are same, they are equal if and only if the corresponding entries are equal. Thus, by comparing the corresponding elements, we get

3x + 4 y = 2, x − 2 y = 4,

a + b = 5,  

and 2a − b = −5.

Solving these equations, we get  x = 2, y = −1, a = 0,  and b = 5.