Definition, Solved Example Problems - General form of a matrix | 11th Mathematics : UNIT 7 : Matrices and Determinants
Chapter: 11th Mathematics : UNIT 7 : Matrices and Determinants
General form of a matrix
General form of a matrix
If a matrix A has m rows and n columns, then it is written as
A = [ aij ]m×n ,1 ≤ i ≤ m,1 ≤ j ≤ n.
That is,

Note that m and n are positive integers.
The following are some examples of matrices :
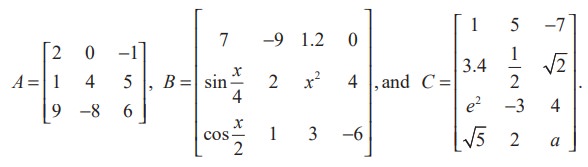
In a matrix, the horizontal lines of elements are known as rows and the vertical lines of elements are known as columns. Thus A has 3 rows and 3 columns, B has 3 rows and 4 columns, and C has 4 rows and 3 columns.
Definition 7.1
If a matrix A has m rows and n columns then the order or size of the matrix A is defined to be m × n (read as m by n).
The objects a11 , a12 , ..., amn are called elements or entries of the matrix A = [aij ]m×n . The element aij is common to ith row and jth column and is called (i, j)th element of A. Observe that the ith row and jth column of A are 1× n and m ×1 matrices respectively and are given by [ai1 a i2 ... a in ] and 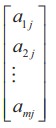
We shall now visualize the representation and construction of matrices for simplifying day-to-day problems.
Illustration 7.1
Consider the marks scored by a student in different subjects and in different terminal examinations. They are exhibited in a tabular form as given below :

This tabulation represents the above information in the form of matrix. What does the entry in the third row and second column represent?
The above information may be represented in the form of a 3 × 5 matrix A as

The entry 84 common to the third row and the second column in the matrix represents the mark scored by the student in English Exam 3.
Example 7.1
Suppose that a matrix has 12 elements. What are the possible orders it can have? What if it has 7 elements?
Solution
The number of elements is the product of number of rows and number of columns. Therefore, we will find all ordered pairs of natural numbers whose product is 12. Thus, all the possible orders of the matrix are 1× 12, 12× 1, 2× 6, 6× 2, 3× 4 and 4× 3.
Since 7 is prime, the only possible orders of the matrix are 1 × 7 and 7 × 1.
Example 7.2
Construct a 2 × 3 matrix whose (i, j)th element is given by
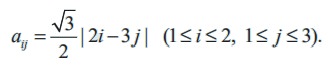
Solution
In general, a 2 × 3 matrix is given by
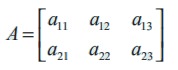
By definition of aij, we easily have a11 = 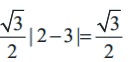 and other entries of the matrix
and other entries of the matrix
A may be computed similarly. Thus, the required matrix A is
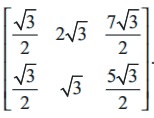
Related Topics