Symmetric and Skew-symmetric Matrices

Symmetric and Skew-symmetric Matrices

Definition 7.17

A square matrix A is said to be symmetric if AT  = A.

That is, A = [ aij ]n×n is a symmetric matrix, then aij  = a ji  for all i and j.

For instance, 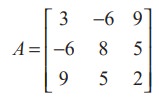is a symmetric matrix since AT =A.

Observe that transpose of AT is the matrix A itself. That is ( AT )T=A.

Definition 7.18

A square matrix A is said to be skew-symmetric if AT  = − A.

If A = [aij ]n×n is a skew-symmetric matrix, then aij  = −a j for all i and j.

Now, if we put i = j, then 2aii  = 0 or aii  = 0 for all i. This means that all the diagonal elements of a skew-symmetric matrix are zero.

For instance, A =

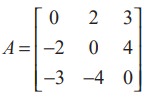
is a skew-symmetric matrix since AT= - A

It is interesting to note that any square matrix can be written as the sum of symmetric and skew-symmetric matrices.

Theorem 7.1

For any square matrix A with real number entries, A + AT is a symmetric matrix and A − AT is a skew-symmetric matrix.

Proof

Let B = A + AT.

BT  = ( A + AT )T  = AT + ( AT )T  = AT + A = A + AT  = B .

This implies A + AT  is a symmetric matrix.

Next, we let C = A − AT . Then we see that

C T  = ( A + ( − AT ))T  = AT + ( − AT )T  = AT − ( AT )T  = AT − A = − ( A − AT ) = − C

This implies A − AT  is a skew-symmetric matrix.

Theorem 7.2

Any square matrix can be expressed as the sum of a symmetric matrix and a skew-symmetric matrix.

Proof

Let A be a square matrix. Then, we can write

From Theorem 7.1, it follows that (A+AT) and (A-AT) are symmetric and skew-symmetric matrices respectively. Since (kA)T = kAT , it follows that 1/2( A + AT ) and 1/2( A − AT ) are symmetric and skew-symmetric matrices, respectively. Now, the desired result follows.

Note 7.4

A matrix which is both symmetric and skew-symmetric is a zero matrix.

Example 7.13

Express the matrix 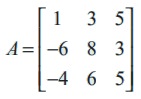as the sum of a symmetric and a skew-symmetric matrices.

Solution

Thus A is expressed as the sum of symmetric and skew-symmetric matrices.