Algebraic Operations on Matrices

Algebraic Operations on Matrices

Basic operations on matrices are

(1) multiplication of a matrix by a scalar,

(2) addition/subtraction of two matrices, and

(3) multiplication of two matrices.

There is no concept of dividing a matrix by another matrix and thus, the operation A/B , where A and B are matrices, is not defined.

(1) Multiplication of a matrix by a scalar

For a given matrix A = [aij ]m×n and a scalar k, we define a new matrix kA = [bij ]m×n , where bij = kaij for all i and j.

For instance, if

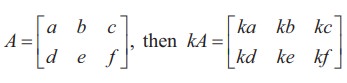
In particular if k = −1 , we obtain − A = [ −aij ]m×n . This - A is called negative of the matrix A.

Don’t say - A as a negative matrix.

(2) Addition and Subtraction of two matrices

If A and B are two matrices of the same order, then their sum denoted by A + B, is again a matrix of same order, obtained by adding the corresponding entries of A and B.

More precisely, if A = [ aij ]m× n and B = [bij ]m×n are two matrices, then the sum A + B of A and B is a matrix given by

A + B = [cij ]m×n  where cij  = aij + bij for all i and j.

Similarly subtraction A - B is defined as A − B = A + ( −1) B.

That is, A − B = [d ij ]m×n , where d ij  = aij − bij  ∀ i and j. (The symbol ∀ denotes for every or for all).

Note 7.2

(i) If A and B are not of the same order, then A + B and A - B are not defined.

(ii) The addition and subtraction can be extended to any finite number of matrices.

Example 7.4

Compute A + B and A - B if

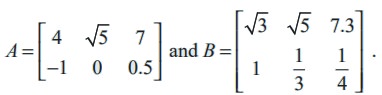
Solution

By the definitions of addition and subtraction of matrices, we have

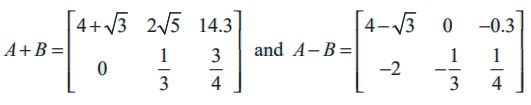
Example 7.5

Find the sum A + B + C  if A, B, C are given by

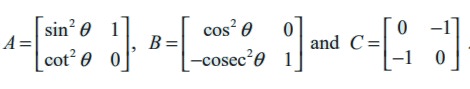
Solution

By the definition of sum of matrices, we have

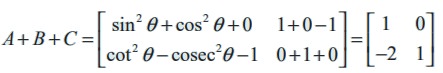
Example 7.6

Determine 3B + 4C - D if B, C, and D are given by

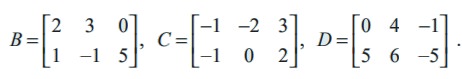
Solution

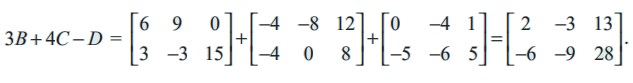
Example 7.7

Simplify :

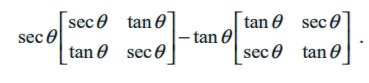
Solution

If we denote the given expression by A, then using the scalar multiplication rule, we get

(3) Multiplication of matrices

Definition 7.15

A matrix A is said to be conformable for multiplication with a matrix B if the number of columns of A is equal to the number of rows of B.

That is, if A = [ a ij ]m× n and B = [b ij]n× p are given two matrices, then the product of matrices A and B is denoted by AB and its order is m × p.

The order of AB is m × p = (number of rows of A)× (number of columns of B).

If A = [a1 a2 ... an ]1×n  and B = ,then AB is a matrix of order 1 × 1, that gives a single element which is defined by

where c11 = 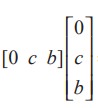 = 0 ⋅ 0 + c ⋅ c + b ⋅ b = c 2 + b2  and other elements cij  may be computed similarly.

Finally, we easily obtain that

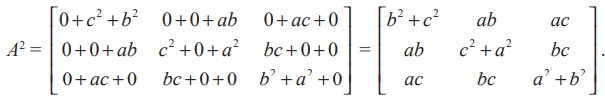
Note 7.3

We have the following important observations:

(1) If A = [aij ]m× n  and B = [bij ]n× p , and m ≠ p, then the product AB is defined but not BA.

(2) The fundamental properties of real numbers namely,

ab = ba ∀a ,b ∈R

ab = ac ⇒ b = c ∀ a,b, c ∈R, a ≠ 0

ab = 0 ⇒ a = 0 or b = 0 ∀ a ,b ∈R

Can we discuss these in matrices also?

(i) Even if AB and BA are defined, then AB = BA is not necessarily true.

For instance, we consider

and observe that AB ≠ BA, since

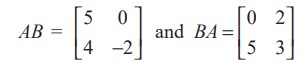
In this case we say that A and B do not commute (with respect to multiplication)

Observe that AB = BA is also possible. For instance,

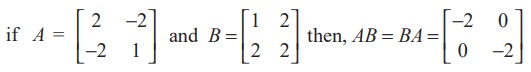
In this case we say that A and B commute with respect to multiplication.

(ii) Cancellation property does not hold for matrix multiplication. That is, A ≠ O, B, and C are three square matrices of same order n × n with n > 1, then AB = AC does not imply B = C and BA = CA does not imply B = C.

As a simple demonstration of these facts, we observe that for instance,

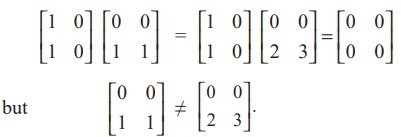
(iii) It is possible that AB = O with A ≠ O and B ≠ O; Equivalently, AB = O is not necessarily imply either A = O or B = O. The following relation demonstrates this fact :

(3) In general, for any two matrices A and B which are conformable for addition and multiplication, for the below operations, we have

(A±B)2  need not be equal to A 2±2 AB  B2

A 2-B2  need not be equal to ( A+B)( A-B).

Example 7.10

Solution

The order of A is 3 × 3 and the order of B is 3 × 2. Therefore the order of AB is 3 × 2. A and B are conformable for the product AB. Call C = AB. Then,

c11 = (first row of A) (first column of B)

Similarly c12 = 0, c21 = 0, c22 = 13, c31 = 7, c32 = 5.

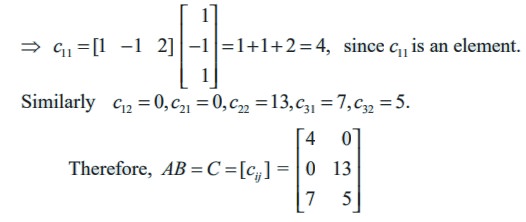
The product BA does not exist, because the number of columns in B is not equal to the number of rows in A.

Example 7.11

A fruit shop keeper prepares 3 different varieties of gift packages. Pack-I contains 6 apples, 3 oranges and 3 pomegranates. Pack-II contains 5 apples, 4 oranges and 4 pomegranates and Pack –III contains 6 apples, 6 oranges and 6 pomegranates. The cost of an apple, an orange and a pomegranate respectively are Rs.  30, Rs. 15 and Rs. 45. What is the cost of preparing each package of fruits?

Solution

Cost matrix A = [30 15 45],

Cost of packages are obtained by computing AB. That is, by multiplying cost of each item in A (cost matrix A) with number of items in B (Fruit matrix B).

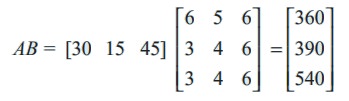
Pack-I cost Rs. 360, Pack-II cost Rs. 390, Pack-III costs Rs. 540.