Determinants: Singular and non-singular Matrices

Singular and non-singular Matrices

Definition 7.21

A square matrix A is said to be singular if | A | = 0. A square matrix A is said to be non-singular if | A | ≠ 0.

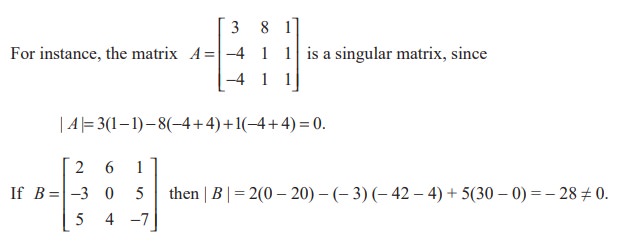
Thus B is a non-singular matrix.

Note 7.14

If A and B are non-singular matrices of the same order then AB and BA are also non-singular matrices because | AB | = | A | | B | = | BA |.

EXERCISE 7.4

(1) Find the area of the triangle whose vertices are (0, 0), (1, 2) and (4, 3).

(2) If (k, 2), (2, 4) and (3, 2) are vertices of the triangle of area 4 square units then determine the value of k.

(3) Identify the singular and non-singular matrices:

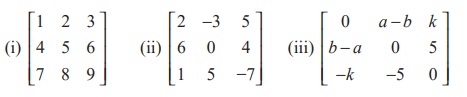
(4) Determine the values of a and b so that the following matrices are singular: