Relation between a Determinant and its Cofactor Determinant

Relation between a Determinant and its Cofactor Determinant

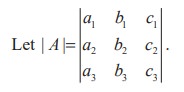
Let A1, B1, C1.... be the cofactors of a1, b1, c1 ... in | A |.

Similarly, | A |= a2 A2 + b2 B2 + c2 C2 And  | A |= a3 A3 + b3 B3 + c3C3

Note that the sum of the product of elements of any row (or column) with their corresponding cofactors is the value of the determinant.

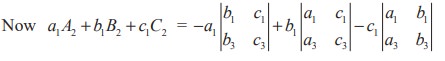
= − a1 (b1c3 − b3 c1 ) + b1 (a1c3 − a3 c1 ) − c1 (a1b3 − a3b1 )

= a1b1c3 + a1b3 c1 + a1b1c3 − a3b1c1 − a1b3 c1 + a3 b1c1 = 0

Similarly we get

a1 A3 + b1 B3 + c1C3  = 0 ;  a2 A1 + b2 B1 + c2 C1 = 0 ;

a2 A3 + b2 B3 + c2 C3= 0 ;  a3 A1 + b3 B1 + c3C1 = 0 and a3 A2 + b3 B2 + c3C2 = 0 .

Note 7.12

If elements of a row (or column) are multiplied with corresponding cofactors of any other row (or column) then their sum is zero.