Determinants: Area of a Triangle

Area of a Triangle

We know that the area of a triangle whose vertices are (x1 , y1 ),(x2 , y 2 ) and (x3 , y3 ) is equal to the absolute value of

1/2 (x1 y 2 − x2 y1 + x2 y3 − x3 y 2 + x3 y1 − x1 y3 ) .

This expression can be written in the form of a determinant as the absolute value of

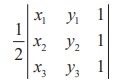
Example 7.32

If the area of the triangle with vertices (- 3, 0), (3, 0) and (0, k) is 9 square units, find the values of k .

Solution

Note 7.13

The area of the triangle formed by three points is zero if and only if the three points are collinear. Also, we remind the reader that the determinant could be negative whereas area is always non-negative.

Example 7.33

Find the area of the triangle whose vertices are (- 2, - 3), (3, 2), and (- 1, - 8).

Solution

Example 7.34

Show that the points (a, b + c), (b, c + a), and (c, a + b) are collinear.

Solution