Definition, Solved Example Problems - Determinants of Matrices of different order | 11th Mathematics : UNIT 7 : Matrices and Determinants
Chapter: 11th Mathematics : UNIT 7 : Matrices and Determinants
Determinants of Matrices of different order
Determinants
To every square matrix A = [aij] of order n, we can associate a number called determinant of the matrix A.
if 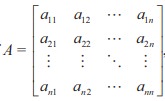 , then determinant of A is written as
, then determinant of A is written as 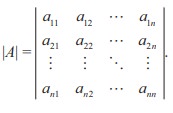
Note 7.5
(i) Determinants can be defined only for square matrices.
(ii) For a square matrix A, |A| is read as determinant of A.
(iii) Matrix is only a representation whereas determinant is a value of a matrix.
Determinants of Matrices of different order
Determinant of a matrix of order 1
Let A = [a] be the matrix of order 1, then the determinant of A is defined as ‘a’.
Determinant of a matrix of order 2
Let A = 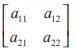 be a matrix of order 2. Then the determinant of A is defined as
be a matrix of order 2. Then the determinant of A is defined as
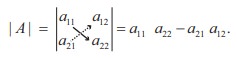
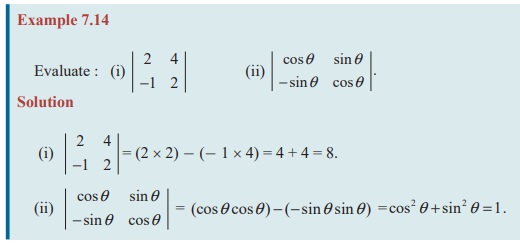
Determinant of a Matrix of order 3
We consider the determinant of a 3 × 3 matrix with entries as real numbers or real valued functions defined on R and study its properties and discuss various methods of evaluation of certain determinants.
Definition 7.19
Let A = [aij ]3×3 be a given square matrix of order 3. The minor of an arbitrary element aij is the determinant obtained by deleting the ith row and jth column in which the element aij stands. The minor of aij is usually denoted by Mij .
Definition 7.20
The cofactor is a signed minor. The cofactor of aij is usually denoted by Aij and is defined as Aij = ( −1)i + j Mij .

Result 7.1 (Laplace Expansion)
For a given matrix A = [aij ]3×3 , the sum of the product of elements of the first row with their corresponding cofactors is the determinant of A.
That is, | A |= a11 A11 + a12 A12 + a13 A13 .
This can also be written using minors. That is, | A |= a11 M 11 − a12 M 12 + a13 M13 .
The determinant can be computed by expanding along any row or column and it is important to note that the value in all cases remains the same. For example,
expansion
along R1 is | A | = a11 A11 + a12 A12 + a13 A13.
along R2 is | A | = a21 A21 + a22 A22 + a23 A23.
along C1 is | A | = a11 A11 + a21 A21 + a31 A31.
Example 7.15
Compute all minors, cofactors of A and hence compute |A| if A = 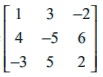
Also check that | A | remains unaltered by expanding along any row or any column.
Solution
Minors:
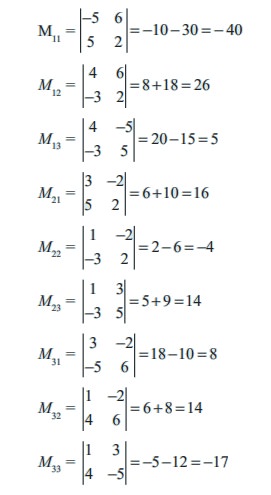
Cofactors :
A11 = (−1)1+1 (−40) = −40
A12 = (−1)1+2 (+26) = −26
A13 = (−1)1+3 (5) = 5
A21 = (−1)2+1 (16) = −16
A22 = (−1)2+2 (−4) = −4
A23 = (−1)2+3 (14) = −14
A31 = (−1)3+1 (8) = 8
A32 = (−1)3+2 (14) = −14
A33 = (−1)3+3 (−17) = −17
Expanding along R1 yields
|A| = a11 A11 + a12 A12 + a13 A13 .
|A| = 1(−40) + (3)(−26) + ( −2)(5) = −128 . ... (3)
Expanding along C1 yields
|A| = a11 A11 + a21 A21 + a31 A31 .
= 1(−40) + 4(−16) + −3(8) = −128 ... (4)
From (3) and (4), we have
|A| obtained by expanding along R1 is equal to expanding along C1 .
Evaluation of determinant of order 3 by using Sarrus Rule (named after the French Mathematician Pierre Frédéic Sarrus)
Write the entries of Matrix A as follows :
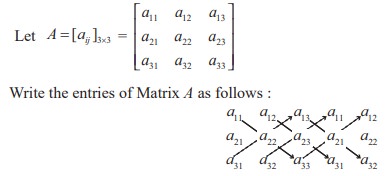
Then | A | is computed as follows :
| A | = [a11 a22 a33 + a12 a23 a31 + a13 a21 a32 ] − [ a33 a21 a12 + a32 a23 a11 + a31 a22 a13 ]

Note 7.6
For easier calculations, we expand the determinant along a row or column which contains maximum number of zeros.
Determinant of square matrix of order n, n ≥ 4
The concept of determinant can be extended to the case of square matrix of order n, n ≥ 4. Let A= [ aij ]n×n , n ≥ 4.
If we delete the ith row and jth column from the matrix of A = [aij ]n×m , we obtain a determinant of order (n −1) , which is called the minor of the element aij. We denote this minor by Mij. The cofactor of the element aij is defined as Aij = ( −1) i + j Mij .
Result 7.2
For a given square matrix A = [aij ]n×n of order n, the sum of the products of elements of the first row with their corresponding cofactors is the determinant of A. That is,
| A |= a11 A11 + a12 A12 + ... + a1n A1n
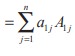
which, by the definition of cofactors and minors, is same as
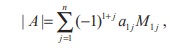
where A1j denotes the cofactor of a1j and M1j denotes the minor of a1j, j = 1, 2, ..., n.
Note 7.7
(i) If A = [aij ]n×n then determinant of A can also be denoted as det(A) or det A or ∆.
(ii) It can be computed by using any row or column.
Related Topics