Theorems on limits

Theorems on limits

The intention of the informal discussion in the earlier section was to have an intuitive grasp of existence or non existence of limit. However, it is neither desirable nor practical in every instance, to reach a conclusion about the existence of a limit based on a graph or table of functional values. We must be able to evaluate a limit, or discern its non existence, in a somewhat mechanical fashion. The theorems that we shall consider in this section establish such a means. The proofs of these theorems are more of technical and are beyond the scope of this textbook.

In Illustration 9.1, we concluded that lim x→2 (x2 + 3) = 22 + 3 = 7. That is, the limit of f(x) = x2 + 3 as  x tends to 2 is equal to f(x) evaluated at x = 2. [That is, f(2)]. However, this process of evaluation, as noted earlier, will not always work because f(x) may not even be defined at x0. Nevertheless, it is true that if f is a polynomial, then it is always possible to calculate the limit by evaluation.

Theorem 9.1

Let P(x) = a0 + a1x + a2x2 + ... + an xn be a polynomial, where a0, a1, ..., an are real numbers and n is a fixed positive integer. Then

The limit of a constant function is that constant.

Theorem 9.2

Theorem 9.3

Theorem 9.4

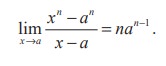
Proof

EXERCISE 9.2

Evaluate the following limits :