Examples of functions Continuous at a point

Examples of functions Continuous at a point

(1) Constant function is continuous at each point of R  

Let f (x ) = k , k ∈ R  is constant. If x0 ∈ R , then f (x0 ) = k.

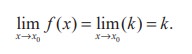
(2) Power functions with positive integer exponents are continuous at every point of R

If f(x) = xn , domain of f is R = (- ∞, ∞) and limx→x0 xn = x0n, x0 ∊ R by the limit theorem.

(3) Polynomial functions, p(x) = a0xn + a1xn-1 +..... an-1x + an  a0≠0

are continuous at every point of R. By limit theorem,

limx→x0 p(x) = a0x0n + a1x0n-1 +..... an-1x0 + an = p(x0)

(4)  Quotients of polynomials namely rational functions of the form

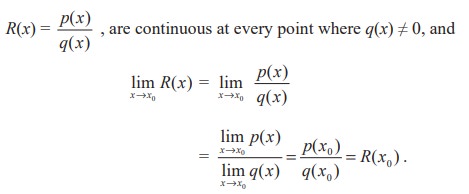
(5)  The circular functions sin x and cos x are continuous at every point of their domain

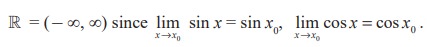
As a consequence, tan x, cot x, cosec x, sec x are continuous on their proper domains in view of the reciprocal and quotient rules in the algebra of limits.

(6) The nth root functions, f(x) = x1/n are continuous in their proper domain since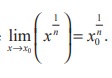

(7) The reciprocal function f (x) = 1/x is not defined at 0 and hence it is not continuous at 0. It is continuous at each point of R −{0} .

(8)

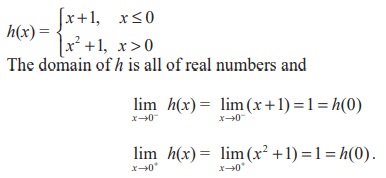
Thus h(x) is continuous at x = 0.

Indeed, h(x) is continuous at each point of (- ∞, 0) and each point of (0, ∞) and hence h is continuous in the whole of (- ∞, ∞).

(9) The greatest integer function f(x) = is not continuous at x = 0.

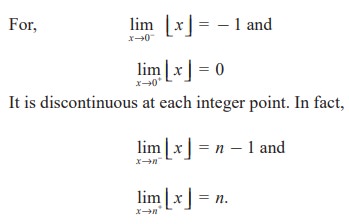
(10) The modulus function

(11) The exponential function f(x) = ex is continuous on R .

(12) The logarithmic function f(x) = log x (x > 0) in continuous in (0, ∞)